概率与测度 (2)：积分与期望

本文属于概率与测度系列。

上一次我们谈到零测集的概念。之所以提出来，一方面是因为它比较好玩，另一方面是它和另一个重要概念息息相关。这个东西就是“几乎处处 (Almost everywhere)”，经常被缩写为“a.e.”。例如，“函数 $f$ 几乎处处等于零”——当我第一次看到这个样子的话的时候，就被深深地雷到了。 =.=bb 当然，我是后来才知道，这个东西是有严格定义的。把一个听起来就模棱两可的词强行加上一个严格的定义，然后直接拿来用，果然搞数学的人好洒脱！

回到 a.e. ，它的定义其实很简单，我们说某个性质“几乎处处”成立，严格地来说，就是在讲它除了在一个零测集上不成立之外，在其他地方都成立。例如，传说中的 Dirichlet function $\chi_\mathbb{Q}$，它在有理数上取值为 1 ，在无理数上取值为 0 （题外话：这个玩意它还是一个处处不连续的函数）。注意到 $\mathbb{Q}$ 的 (Lebesgue) 测度为零的，因此 $\chi_\mathbb{Q}$ 除了在一个零测集上之外，其他地方都取值为零，那么我们就说它“几乎处处为零”。

和这个对应的概率论里常用的还有一个看起来更雷人的概念，叫做 almost surely (或者叫做 almost certain 、almost always) ，说某件事情 almost surely 成立，就是说这件事情在一个“满测度”集合上成立。所谓“满测度”集就是说它的补集的测度为零，而并不一定要求补集是空集。不过零测集和空集之间的关系，如果不严加定义的话，仅用文字描述起来很难搅清楚，而用上了 almost surely 这样的看起来很模糊的词，就更加雪上加霜了。也许，都是那些数学工作者的错——选了一些表面上看起来很混淆的用词，结果导致一些人在并不知道真正严格含义的情况下纠缠在字面上的意思，最终沦落为民科啊……

当然，抛开用词不说，a.e. 的引入在实分析中是必要的——而并不只是简单的把原来的一些“处处成立”的定理推广为“几乎处处成立”这样一个看上去无关痛痒的扩展。可以想像一下，应该是某个定理在条件中不是 a.e. ，但是结论只能得到 a.e. ，所以说如果去掉 a.e. 这个概念的话，整条路就走不通了。不过，这里暂时还没法详细说这个问题。于是下面以一幅 6 格漫画结束开场白，正式进入这次的主题——“积分”吧！

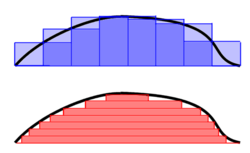微积分现在几乎是所有专业的大一必修课了吧，在微积分课程里讲积分的时候，我们都还记得，积分就是用一堆长方形条来近似一个函数图像“下”面的面积——如右图中蓝色的那个图。这样的积分叫做黎曼积分 (Riemann Integral)，而这次要讲的积分叫做勒贝格积分 (Lebesgue Integral) ，一般最常用的示意图是右边红色的那个。从对比图中可以看到，黎曼积分是对定义域进行划分，而勒贝格积分是对值域进行划分。表面上看起来似乎是一个比较无聊的变化，但是实际上这个简单的变化使得勒贝格积分的应用范围相对于黎曼积分来说大大推广了。

当然，对于我们普通的实函数 $f:\mathbb{R}\rightarrow\mathbb{R}$ 来说，似乎直观上看不出太大的区别（稍后我们会说，即使这种情况下也是有很大区别的），但是考虑推广的概念：$f:\mathcal{X}\rightarrow\mathcal{Y}$ 称为一个映射，如果对于每一个 $x\in\mathcal{X}$ ，由 $f$ 给定一个 $f(x)\in\mathcal{Y}$ 。这里 $\mathcal{X}$ 和 $\mathcal{Y}$ 分别称为映射的定义域和值域，当值域是 $\mathbb{R}$ 或者其子集时，我们通常将映射称为“函数”。也就是说，我们可以在一个抽象的空间中定义函数，但是如果要对这样的函数进行积分的话，黎曼积分就派不上用场了，因为你没有办法直接在一个抽象的空间里做“划分”，但是勒贝格积分却可以做，因为对于一个“函数”来说，值域总是实数，在实数集上做划分是我们已经熟知的工作。

当然，除了这一个直观上显而易见的好处之外，勒贝格积分相对于黎曼积分还有一大堆优点——当然，黎曼积分也有它自己的优点，最明显的一个大概就是它是方便计算的吧，大部分函数直接按照勒贝格积分的定义来进行计算会是相当繁琐的一件事情（幸运的是当一个函数是黎曼可积的时候，它的黎曼积分和勒贝格积分是相等的），我想这也许是微积分里要讲黎曼积分而不是直接讲勒贝格积分的原因吧，在实际中会更有用一点，而且也不需要测度方面的准备知识就能讲。

不过，如果我们想要在抽象的集合上定义概率的若干基本概念，就必须要用勒贝格积分。前面的直观解释虽然看起来还蛮简单的，但是对值域进行划分也并不是简单地将“对定义域进行划分”的方法类比过来就行得通的，因为对于一个自变量，总是只有唯一的函数值，但是反过来，对于一个函数值，却有可能会有许多自变量与它对应。具体地操作起来，还需要借助于测度这个工具。

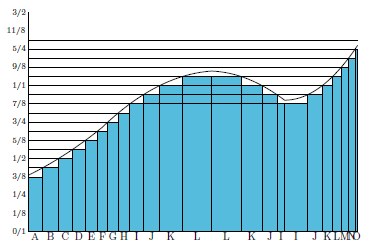不过，我不知道为什么众多关于勒贝格积分的示意图都被画成我刚才展示的那张图那个样子（上面那张图来自于 wikipedia ），每次看到那张图我都会觉得非常 confusing 。左边这张图应该更为贴切一点：虽然按照值域进行了划分，但是最后得到的还是一个一个的“竖着的”（而不是像上面的图中那样“横着的”）矩形相加。比如，对于值域的某个区间 $I=[c,d]$ ，我们记（注意这只是一个记号，与 $f$ 是否有反函数没有关系）：

\[
f^{-1}(I) = \{x|f(x)\in I\}
\]

如果这个集合可测的话，那么我们用它的测度 $m(f^{-1}(I))$ 乘以“高度” $c$ ，就得到了一块面积。不过这块面积并不一定是一个矩形的面积，它可能对应许多个矩形，取决于集合 $f^{-1}(I)$ 的形状，如果它是一个单一的区间的话，那么就只对应一个矩形。不过现在的好处是，我们不用关心它的形状是什么，只要测度可以算出来就可以了。

白话解释已经足够多了，下面我们来把整个过程说得稍微更精确一些。以下除非特别指明，都用“积分”来简称“勒贝格积分”。首先我们要引入“可测函数”的概念。称一个函数 $f$ 是可测的，如果它的定义域是一个可测集，并且对于任意的 $y_0$ ，集合 $\{x|f(x) < y_0\}$ 是可测的。根据可测集构成一个 $\sigma$-algebra 的性质，还能导出如果 $f$ 是可测的，那么 $\{x|f(x)\leq y_0\}$ 、$\{x|f(x) > y_0\}$ 、$\{x|f(x)\geq y_0\}$ 等这些集合也都是可测的，这样一来，我们刚才的集合 $f^{-1}(I)=\{x|c\leq f(x)\leq d\}$ 也是可测的——如果不可测的话，我们就没有办法算积分了。因此，我们的积分整个都是建立在可测函数的基础之上的——这并不是一个很大的限制，因为很多“有用”的函数都是可测的，包括一切（定义域为可测集的）连续函数等等。另外，可测函数的加和、乘积以及（几乎处处）逐点收敛的极限都还是可测的。

在可测函数中，有一类性质非常优良的函数，叫做简单函数 (Simple function) 。简单函数是一个取值为实数的可测函数，并且它的函数值只有有限个。例如，我们一开始提到的 Dirichlet function 就是一个简单函数，因为它的函数值只有 0 和 1 这两个值（并且显然还是可测的）。事实上，我们在那里用了个比较奇怪的记号 $\chi_\mathbb{Q}$ ，这个实际上是一类叫做 indicator function 的函数的通用记号（另外也常记作 $\mathbf{1}_\mathbb{Q}$ ）。一个集合 $A$ 的 indicator function 是这样一个函数：

\[
\chi_A(x) = \begin{cases} 1 &\text{if } x \in A, \\ 0 &\text{if } x \notin A. \end{cases}
\]

所以 Dirichlet function 实际上是有理数集的 indicator function 。用 indicator function 可以很容易来描述一个简单函数，假设简单函数 $\phi$ 的所有取值为 $c_1,\ldots,c_n$ ，则我们有

\[
\phi(x) = \sum_{i=1}^n c_i\chi_{E_i}, \quad E_i=f^{-1}(\{c_i\})
\]

简单函数乍看起来似乎不太简单，特别是像 Dirichlet function 这种处处不连续的函数居然也能混个简单函数的“户口”。不过对于定义勒贝格积分来说，简单函数确实是再简单不过了。首先我们从定义域的测度有限的情况开始考虑，如果 $\phi$ 是个如上形式的简单函数，它的定义域为 $E$ 并且 $m(E) < \infty$ ，我们直接定义它的积分为 \[ \int_E \phi = \sum_{i=1}^n c_i m(E_i) \] 正是我们一开始白话中说的，将值域进行划分——由于这里的函数值只取有限个点，所以直接采用了最简单的单点划分，然后我们直接将每个函数值对应的定义域区间的测度相乘，再全部加起来就得到了。并且由于 $m(E) < \infty$ ，由测度的单调性知道每个 $m(E_i) < \infty$ ，因此定义式的右边也不会出现无穷大这样的情况。有了这个工具，我们可以就可以计算 Dirichlet function 在某一个测度有限的可测集上的积分了，例如： \[ \int_{[0,1]}\chi_\mathbb{Q} = 1\cdot m([0,1]\cap \mathbb{Q}) = 0 \] 到这里，勒贝格积分的最原始形式就已经初露锋芒了：Dirichlet function 这个东西由于太不连续了，黎曼积分是无法对它进行处理的。选择简单函数作为起点，一个是因为它简单，另一个是因为它性质非常好：对于任意一个定义在可测集 $E$ （并没有要求测度有限）上的可测函数 $f$ ，存在 $E$ 上的一列简单函数 $\{\phi_n\}$ 逐点收敛于 $f$ ，并且满足 $|\phi_n|\leq|f|$ 。如果 $f$ 是非负函数的话，还能做到这一列简单函数是单增收敛于它的，这一点性质很好，利用这个，我们可以来定义非负可测函数的积分： \[ \int_E f = \lim_{n\rightarrow \infty}\int_E\phi_n \] 这里 $f$ 是一个非负的可测函数，而 $\{\phi_n\}$ 是一列单增收敛与 $f$ 的简单函数。可以证明，右边的极限总是存在的（如果把趋向于 $+\infty$ 也看成极限存在的话），并且，还能证明右边的极限并不依赖于特定的函数列 $\{\phi_n\}$ 的选取。这样一来，非负可测函数的积分就定义好了。当这个积分小于 $+\infty$ 的时候，我们称 $f$ 是（勒贝格）可积的。 最后，只要再推广到任意可测函数就大功告成啦！而这个推广也是非常简单的，对于任意可测函数 $f$ ，我们可以把它分解为正部和负部：$f=f^+ - f^-$ ，其中 \[ \begin{aligned} f^+(x) &= \max \{f(x),0\} \\ f^-(x) &= \max \{-f(x),0\} \end{aligned} \] 都是非负可测函数，很自然地，我们希望将 $f$ 的积分就定义为 \[ \int_E f = \int_E f^+ - \int_E f^- \] 不过如果 $\int_E f^+$ 和 $\int_E f^-$ 同时为 $\infty$ 的话，这个式子就没有意义了。因此我们做一点限制，注意到 $|f|=f^+ + f^-$ 也是一个非负可测函数，如果 $|f|$ 可积的话，可以得到 $f^+$ 和 $f^-$ 都是可积的（反之也对），这个时候上面的式子就不会出现无穷相减的问题。因此，对于任意可测函数 $f$ ，当非负可测函数 $|f|$ 是可积的时候，我们称 $f$ 是可积的，并用上面那个式子来定义它的积分。这样一来，我们的勒贝格积分终于定义好了！ 😀 勒贝格积分相对于黎曼积分有诸多好处，例如，$|f|$ 可积当且仅当 $f$ 是可积的，但是黎曼积分得不到这个性质，还有通过控制收敛定理可以得到（收到控制的）可积函数的（几乎处处收敛的）极限也是可积的，并且极限的积分等于积分的极限。顺带一提，控制收敛定理的条件中只要求 a.e. ，这是一个重要的细节，如果不能保证只要在 a.e. 的时候就能成立的话，基于 Lebesgue 积分的后续一些理论就会出现困难了。如果以后有讲到这个内容再细说吧。

接下来让我们迫不及待地进入概率论的话题，当然其实也只是一个很小的序幕，把我们之前介绍过的测度和积分用一下，建立一些基础设施。不过这里其实也是非常简单的框架，在后续的介绍中说不定还会有一些变动。直接进入正题吧！首先是“概率空间”，其实就是一个特殊的测度空间： $(\Omega,\mathcal{A},P)$ ，其中 $\Omega$ 就是一个集合，然后 $\mathcal{A}$ 是可测集组成的集合（它是一个 $\sigma$-Algebra ），而 $P$ 是一个测度，这里我们额外要求 $P(\Omega)=1$ ，即全集的测度是有限并且归一化的。顺带一提，本文开头谈到的事件 $A$ almost surely 成立，到这里就有明确的意义了，其实就是 $P(A)=1$ 。

在这种情况下，我们引入一些新的名词：归一化的测度 $P$ 被称作“概率”，$\mathcal{A}$ 里的那些可测集，被称作“事件”，而 $P(A)$ 就是事件 $A$ 的概率了。下面举一个例子，考虑扔骰子，这个时候我们的对象集合包含了 1 到 6 这 6 个数码。接下来我们要在这个集合上定义一个测度。比如，我们尝试把它看成是实数集的一个子集，然后用我们之前说过的 Lebesgue 测度限制到这个集合上，可是我们知道勒贝格测度在有限集上的测度总是为零，对我们没有什么用，并且也没法满足归一化的条件。于是我们考虑另一种更适合这种情况的测度：counting measure ，也许可以翻译做“计数测度”吧，顾名思义，它就是通过数对象的个数来计算测度的，在有限集上特别好用，它的定义为：

\[
P(\{x_1,…,x_n\}) = n
\]

或者也有推广的定义，使得每个元素可以有一个权重：

\[
P(\{x_1,…,x_n\})=\sum_{i=1}^nw_ix_i
\]

接下来我们将它进行归一化，定义 $\tilde{P}(A) = P(A)/P(\Omega)$ 。注意我们的 $\Omega$ 是个有限集，并且我们定义的这个测度在 $\Omega$ 的所有子集上都可用的，所以可测集（也就是事件集合）就是所有子集。这样一来，我们的测度空间就构造好了，不妨设我们选取了不带权重的计数测度并进行了归一化，还记为 $P$ 。简单地计算就可以验证，这个玩意就和我们熟知的扔骰子的概率模型是一样的，比如：

\[
P(\{1\})=P(\{2\})=\ldots=P(\{6\})=\frac{1}{6}
\]

不过这样似乎有点小题大做了，不过这个框架确实可以对问题统一地描述，下面再来看一个稍微抽象一点的例子，这个时候取集合 $\Omega=[0,1]$ 为一个区间，并且直接用勒贝格测度 $m$ 和 $\mathbb{R}$ 上所有的勒贝格可测集和 $[0,1]$ 的交构成事件集合（注意这个测度已经自动归一化了）。这样我们实际上就得到了一个——用我们熟悉的概率论的语言来说的话——在 $[0,1]$ 区间上的均匀分布。这个例子有点无聊，不过我想说的是，现在对于 $[0,1]$ 区间上的任意一个数 $x$ ，我们总是有 $m(\{x\}= 0$ （勒贝格测度在可数集上总是零），这就解释了我在上一篇中提到的那个从小就困惑我的问题：为什么在连续情况下我们不去谈论 $P(x=x_0)$ ，或者说为什么它是等于零的。 🙂

接下来让我们再引入几个其他我们已经耳熟能详的名词——至少不能把费了这么大力气介绍的勒贝格积分给冷落了啊。在一个测度空间下的一个可测函数，我们把它叫做随机变量。事实上，我们可以把之前定义的“可测函数”的概念加以推广，到“可测映射”的情况，考虑两个测度空间 $(A,\mathcal{A},\mu)$ 和 $(B,\mathcal{B},\eta)$ ，以及他们之间的一个映射 $\xi$ ，如果对于 $B$ 中的可测集 $S\in\mathcal{B}$ ，我们总有 $\xi^{-1}(S)$ 在 $A$ 中可测，即 $\xi^{-1}(S)\in \mathcal{A}$ ，那么称 $\xi$ 是从 $A$ 到 $B$ 的一个可测映射。注意如果将空间 $B$ 取为实数集 $\mathcal{R}$ 加上勒贝格测度，并取 Borel 集作为可测集，那么此时的可测映射就和我们之前定义的可测函数是等价的——也就是随机变量了。

另外一些常见的情况，如果空间 $B$ 是 $\mathbb{R}^d$，称为随机向量，是无穷维 $\mathcal{R}^\infty$ 时称为随机序列，而当 $B$ 是一个函数空间时，则引出随机过程的概念。特别地，如果 $\xi$ 是一个简单函数——回忆一下定义，它的函数值只有有限个，那么我们得到所谓的离散型随机变量。

对于任意 $S\in\mathcal{B}$ ，由于 $\xi^{-1}(B)$ 是可测的，因此我们可以计算测度 $\mu(\xi^{-1}(B))$ ，通常情况下，我们还是将空间 $A$ 取作 $[0,1]$ ，而将勒贝格测度限制在该区间上得到归一化的测度 $P=m|_{[0,1]}$ 。这个时候我们称函数复合 $L=P\circ \xi^{-1}$ 为随机变量（向量、过程、等等，统称随机元）的分布 (distribution) ，对于随机变量的情况，就是我们熟知的概率分布函数啦！

呃，似乎还是没有用到积分……其实积分是被用来引入期望了，一个随机元的期望定义为

\[
\mathbb{E}\xi = \int_{[0,1]}\xi
\]

例如，对于一个离散型随机变量，设 $\xi$ 为一个简单函数 $\xi(x)=\sum_{i=1}^n a_i\chi_{E_i}(x)$ ，那么其期望为

\[
\mathbb{E}\xi = \sum_{i=1}^n a_i m(E_i)
\]

也和熟知的离散型随机变量的期望定义是一致的。暂时不想举更多的例子了，于是一切要在此戛然而止了，篇幅也已经比较长了，后续的内容，大概要作为正式学习概率论的笔记的形式出现了吧。