训练数据对分类器性能的影响

之前一个朋友托我试验一下训练数据的不平衡性对分类器会有多大影响，他所用的分类器是支持向量机（SVM），用来做文本分类。这本身是一个已经研究得比较多的领域了，也已经有比较成熟甚至可以直接在生产中使用的工具（比如这里要用的 LIBSVM）了。当然分类器是由训练数据训练出来的模型，所以训练数据肯定会对其造成直接的影响，这里所说的不平衡性就是各个类别的训练 sample 数目不平衡，比如，在二元分类的情况下，有 1000 个正例和 1 个反例，这就是严重的不平衡。正好最近实验室要做的实验也和这有点关系，我就动手试验了一下训练数据对分类器的性能的影响。有一点要说明的是，这里的“性能 (Performance)”并不是程序的运行时间和效率那个意思，特定到分类的问题上，我们可以用某一个指定的指标（比如 precision 、accuracy、error rate 等）来对结果进行衡量，衡量的结果的好坏，就是这个算法的 performance 。虽然有点难以接受，但是似乎做 research 的时候算法从“运行时间”这个角度来讲的“性能”通常都不在考虑范围之内。^_^bb

虽然其实道理对于所有的分类器都适用，但是因为这里是专门针对 SVM (Support Vector Machine) 来讲的，所以还是先简单介绍一下 SVM 吧。同众多其他流行的分类器一样，SVM 通过一个 hyperplane 来分开数据，在二维空间上就是一条直线，如下图中三条绿色的直线都是合理的 hyperplane ：

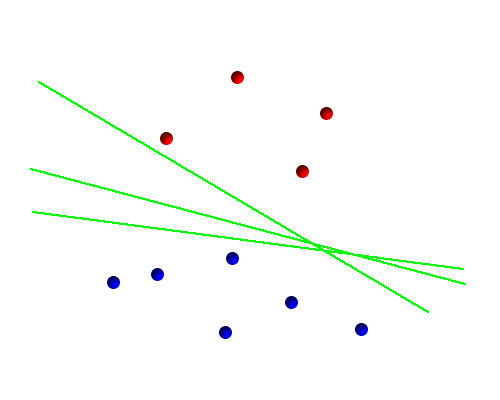
对于需要复杂的“曲线”边界才能分开的情况，通过将数据映射到高维空间中通常都能转化为可以用线性边界分开的情况，这个过程通常使用 Kernel Trick 来完成，不过这些不是今天要说的话题。从上图中看到，这里其实可以有无穷多个“合理”的超平面，但是我们需要从中选一个。SVM 的特殊之处就在于它选择了那个能使 margin 最大化的超平面，如下图所示：

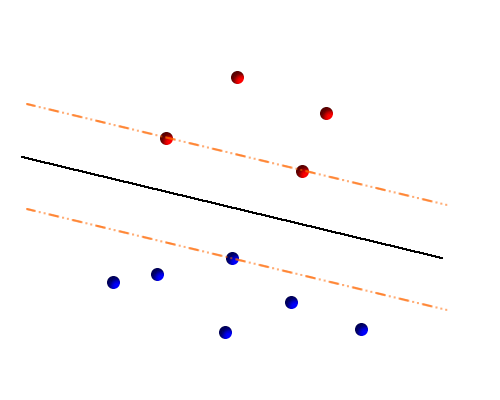
margin 就是超平面到离它最近的点的距离，图中黑线到橙色虚线的距离，SVM 在不同位置和方向的超平面之中选择了黑色的这个，因为它的 margin 最大（图是手工画的，所以也许不是很准确，但是就是那个意思）。这样做有不少好处，其中之一就是现在 SVM 只要集中关注在边缘上的那些点，亦即图中橙色虚线上的点，这些点被称作 Support Vector （因为每一个数据实际是被表示成一个 D 维向量的），这也是 Support Vector Machine 这个名字的由来。图中的训练数据一共有十个，而 SVM 只需要利用其中三个，其他的则直接无视，这在数据量变得非常大的时候可以很有效地减少计算复杂度。

另一方面，SVM 在实践中也被证明性能非常好，我在谈 Gaussian Mixture Model 的那篇文章中曾经讲过归纳偏执和过拟合的问题，对这里同样适用。最开始我们说有无数个“合理”的超平面，说合理是因为他们能把这十个点按照颜色完美地分开，然而这并不代表所有的超平面都能有很好的 generalization ——在训练数据（也就是这十个点）上表现好并不一定总是能在未知的测试数据上表现良好。而 SVM 的归纳偏执可以看成是“margin 最大的 hyperplane 才是最好的”，实践证明，这看上去颇有些 naive 的偏执表现很好，优异的 generalization 让它在手写识别、图像减速、文本分类等许多领域都得到了广泛应用。

除此之外，在上面的例子中，由于训练数据中的 70% 实际上最终是没有什么用的，可以想像，如果“运气好”的话，刚好找到那三个 Support Vector ，直接把它们拿去做训练，一点都不浪费！这个想法是非常诱人的，因为在许多领域，要收集带 label 的训练数据通常代价都比较昂贵——需要人工进行标记。

好了，一不小心打了这么多 SVM 的广告，准备工作也差不多了，下面进入今天的正题：不平衡的训练数据。实际上这种情况还比较常见，比如医院收集了病人的特征，想训练出一个分类器来分出病人是“生病”还是“正常”，可是，去正常人谁没事去医院看病啊？这样一来，医院收集到的训练数据肯定大部分是打有“生病”标签的 sample 。

那么这种不平衡的训练数据会不会对分类器的性能造成影响呢？自觉肯定是“会”，再仔细想想，还是“会”！让我们从直观上来想一想，假设分类问题有一个“绝对真实”的 true hyperplane ，当然，我们是不知道 true hyperplane 的，而我们用 SVM 来寻找 max margin hyperplane 的目的就是为了要近似这个 true hyperplane ，我们随机地选一些点作为训练数据，那么自然是选的点数越多，越有可能选到接近真实 margin 的点；相反，如果只有很少的点，那么选到真实 margin 上的概率就变小了许多，从而近似 true hyperplane 的可能性也降低了。而在真实数据中，即便排除各种误差造成的奇怪数据的影响，大部分问题实际也还并不是可分的（这里的问题是数据的重叠，即使是理论上能实现的最好情况也不能达到 100% 的精确度），数据少的一方很容易受到另一方的“压制”。

下面不妨来实际实验一下。我们使用 20 Newsgroup 这个数据集来做一下实验。这是从新闻组上收集的按照主题分类的文本，在文本分类领域里是一个很经典的数据集。这里我们直接使用蔡登提取好 feature 的数据，并选了其中的两类来进行实验——这样，我们的实验数据是 1985 个 8014 维的向量。

实验使用 Cross Validation 的做法，将数据随机地分为五份，每次选其中的 4/5 作为训练数据集，其余的 1/5 作为测试集，重复五次，统计分类器在测试集上的 accuracy ，最后求得五次的平均值作为衡量的指标。

不同的是，我们这里并不是把训练集中的所有数据都拿来训练。为了实验训练数据的影响，我们先初始地选正反数据各两例，训练出一个初始的模型，然后逐步地增加训练数据，并重新训练模型，最后可以得到一个横坐标为训练数据个数，纵坐标为 accuracy 的图来：

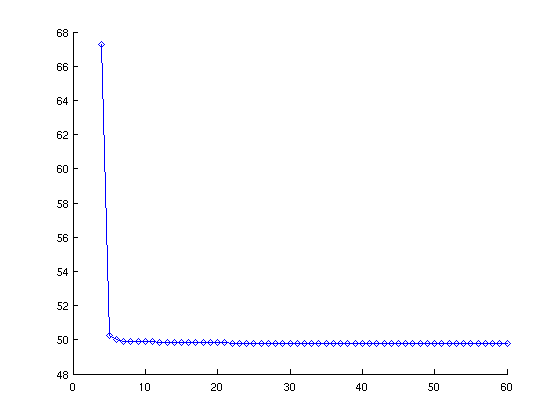
这个图看起来比较诡异 ，怎么会随着训练数据的增加 accuracy 反而下降呢？没错，正是因为我在这里做了手脚 :p 。事实上，我在这里用了一种特殊的选取训练数据的方式：只选取某一个 category 的数据，目的是产生训练数据不平衡的情况。从途中可以看到，初始的时候是我们随机选了正反各两个训练数据，accuracy 能够达到 67% 左右，然而随着我们选取更多的（同类的）数据，精度急剧下降，最后“稳定”在 50% 左右。事实上，对于一个二元的分类器来说，没有什么比 accuracy 低于 50% 更丢脸的事了，因为我只要把它的分类结果完全颠倒过来就能达到比它更好的结果。不妨再来看看和随机地选取实验数据的对比：

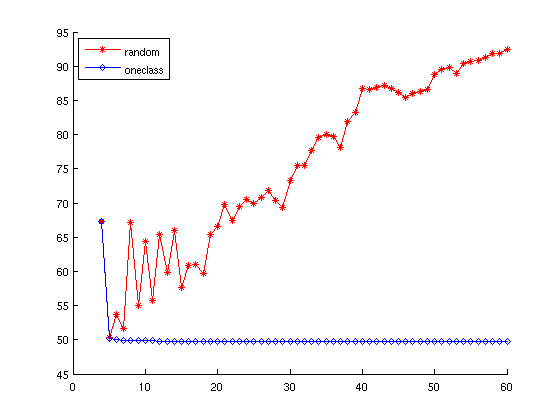
可以看到，虽然一开始有点波动（因为初始的训练数据只有四个点，很容易受到影响），但是总体的趋势显然是和单类选点的方式走了完全不同的路线。这说明，不平衡的训练数据通常会降低分类器的性能，当然至于影响有多大，必然是不能一概而论的了，而解决这个问题的办法一般有两种：

1. 从实验数据上做文章，这中方法又再细分为两种：
   • under sample: 简单地说就是把 sample 太多的那个类的训练数据去掉一些，通常我们会选一些诸如孤立点啊之类的看起来不太顺眼的数据丢掉。想想，对于上面那个例子，把后面选出来的点全部丢掉，只留下最开始的那 4 个训练数据，还能达到 67% 的 accuracy 呢，至少比 50% 要好。
   • over sample: 也就是增加 sample 少的一类的数据了，最直接的方法当然是人工标注更多的训练数据了，还有一些不需要人工标注的方法，比如简单地 copy & paste 让数据重复 N 次，或者利用“相似的数据其 label 肯定也相似”的想法，捏造一些数据出来，给自动标上 label 等等。
2. 从分类算法上做文章。比如 SVM ，基本上能活动的地方都被人拧了拧，只要能把“我希望你不要歧视小众”这个美好愿望传达过去，结合到最终模型中，都可以算一种方法。比如，有一种最土的办法是在训练完成之后再偷偷地把 hyperplane 往另一边挪一下。而其他看起来靠谱一点的方法却又有些复杂了（比如 moonykily 前几天给我看的这篇 Class-Boundary Alignment for Imbalanced Dataset Learning 就是在 Kernel Function/Matrix 上做手脚），我也没有亲自试过。但无疑每个提出方法并发表了论文的人的方法肯定都是“比其他方法要好”的。 ^_^

Vladimir Vapnik

到此为止，似乎问题解决了——话是不假，不过新的问题又来了，到底要如何处理这种情况呢？上面列了一些解决方案，简单的看起来太土了，都不好意思用；复杂的看起来又太学术了，难保在实际中效果好不好。确实，在实际中，如果可能的话，大概最合适的解决办法还是老老实实地为 sample 少的一方增加训练数据吧，比如医院也可以开个救护车去大街上，免费为大家提供体检之类的服务，趁机多收集一点正常人的数据。

当然，医院这个例子除了标记 label （也就是进行诊断了）很费力之外，仅仅是收集 unlabeled data 就相当麻烦。更常见的情况是收集 unlabeled data 相当容易，最典型的例子是抓取网页，只要让爬虫自己在后台不断去抓就可以了（当然，我们这里省略写一个优秀的爬虫说需要的精力，毕竟从某种意义上来说是一劳永逸的嘛），但是要为爬下来的网页分类，却实在是个麻烦活，而且也很无聊，特别是想到我辛辛苦苦地标记的数据有可能在 Support Vector 的海选中惨遭淘汰，做起事来就是千万个不愿意了。如果能让我标记的 sample 全部入选 Support Vector 的话，我一定每天给 Vapnik 老爷爷上三柱香！ :p

不过，说起 Support Vector Machine 之父 Vladimir Vapnik ，一定要允许我多嘴一句句，这里有一个小小的八卦：SVM 是 Vapnik 在 AT&T Bell 实验室的时候提出来的——那个群牛云集的地方相信大家都不陌生了。原始照片在这里，白板里的文字是“All your Bayes are belong to us”，至于公式嘛，我也不知道是不是某个具体的公式，不过既然是通过 Empirical Risk 来估计真实 Risk 的上限，猜想应该是和 VC 理论 或者 VC 维 相关的东西吧，这可是解决我们前面多次谈到的“过拟合”以及 generalization 问题的有效理论工具哦，不过我现在还不懂。 ^_^bb

好了，八卦完毕，回归正题，由于 Vapnik 他老人家现在还相当硬朗，烧香大概还是没有什么用了。不过其实仔细想想还是有办法的，不信你使劲拍拍自己的脑袋！想想，我们不是已经有了一个 SVM 了，要选更多的 sample 吗？我们不是想要新加入的点都尽可能地变成 Support Vector 吗？那么 Support Vector 在哪里呢？靠近 hyperplane 的地方！bingo! 我们只要在收集到的所有 unlabeled data 中选取离 hyperplane 最近的一些点，标记一下，那么它们成为 Support Vector 的概率就很大了，并且结果很有可能比之前的 hyperplane 更好，然后我们可以用迭代的方法来选更多的点。

下面我用一个简单的例子来说明一下这种选点的方法：因为二维数据很容易 visualize 出来，所以我使用两个二维 Gaussian 分布生成的数据，就是下图中黄颜色的点，大致可以看出他们分成左右两“团”，并有不同的 label 。而蓝颜色的四个点是初始选的点——正反各两个，可以看到左边一类的有一个初始点被随机到了很边缘的地方，甚至都在右边的大本营了，不过这不是重点。我这里主要想展示的是红颜色的点——有目的地选择的靠近 hyperplane 的点和绿颜色的点——完全随机选出来的点：

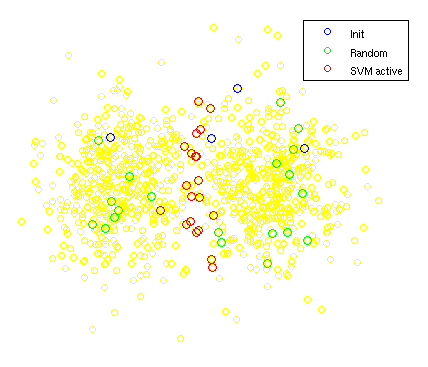
可以看到我们的目的已经达到了，选了很多靠近 hyperplane 的点（虽然我没有把它画出来，但是 hyperplane 就在中间应该没有异议吧？），这在 LIBSVM 中其实很容易实现，用它提供的 svmpredict 方法，返回的第三个结果就是数据离 hyperplane 的距离，正负分别表示在 hyperplane 的两边：

[lbls accur dec_vals] = libsvm.svmpredict(gnd, fea, model);
[dummy I] = sort(abs(dec_vals));
idx = I(1:n); % select n sample nearest to hyperplane

那么效果如何呢？自然是不错的！不过用这个合成的数据做实验的结果并不是很有说服力，让我们再回过头来用之前提到的 20 Newsgroup 的数据来对比一下：

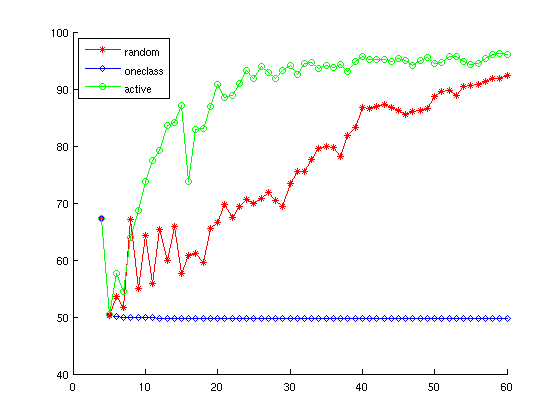
上图中绿线就是这种方法选 sample 得到的结果，很不错吧？ 😀 图中给的标签是 active ，来自于 Active Learning ，此 Active Learning 并不是教育学中的那个 Active Learning （虽然其实名字还是来源于此吧），而是 Machine Learning 中的一个子领域，用统计学的黑话来说就叫做 Experimental Design ，要解决的就是我们这里面临的问题：如何从 unlabeled data 中选出“重要”的 sample 来进行标记并用做下一步的训练数据。

而这里用到的这种看起来相当启发式的方法（“启发式”一词似乎在 Machine Learning 里面略带贬义，有点“没有理论基础”的味道）其实也是有比较严格的理论依据的（请参考 Support Vector Machine Active Learning with Applications to Text Classification 这篇论文），也许你已经猜到了，它实际上是众多 Active Learning 中比较土的一种方法，通常被称为 Simple Margin 或者其他名字（程序员有时会对不统一的变量名和函数名感到非常恼火，对应到搞 research 的人身上，大概就要数不统一的数学符号和算法名了吧）。不过今天就不再对 Active Learning 展开来多讲了，感兴趣的同学可以参考一下这个 Survey ：Active Learning Literature Survey 。不过这个子领域其实最近也还在不断地提出一些新的方法，还是比较活跃的。

最后，Simple Margin 虽然从理论上来讲有点土，但是实际表现还是不错的，所以，用这样的办法来完善 sample 少的类别的训练数据，大致也算是为这个烦人的问题提出了一个解决办法。另外，除了离 hyperplane 最近的点之外，我们也可以利用离 hyperplane 最远的点：实际上离 hyperplane 的距离可以看作是 SVM 对自己 predict 出来的 label 的 confidence ，最远的点一般会被一个正常的 SVM predict 的概率可以说是非常小了，所以，我们可以直接采取完全信任的方式，将 SVM predict 出来的 label 直接作为其“真实” label ——这样可以达到一个不需要人工标记的收集 labeled data 的目的。当然，这样收集得来的数据通常并不如人工标记的那些离 hyperplane 近的那些点的作用那么大，但是至少可以拿来做一个测试集吧。 🙂