 本文是“漫谈 Clustering 系列”中的第 4 篇,参见本系列的其他文章。
本文是“漫谈 Clustering 系列”中的第 4 篇,参见本系列的其他文章。
上一次我们谈到了用 k-means 进行聚类的方法,这次我们来说一下另一个很流行的算法:Gaussian Mixture Model (GMM)。事实上,GMM 和 k-means 很像,不过 GMM 是学习出一些概率密度函数来(所以 GMM 除了用在 clustering 上之外,还经常被用于 density estimation ),简单地说,k-means 的结果是每个数据点被 assign 到其中某一个 cluster 了,而 GMM 则给出这些数据点被 assign 到每个 cluster 的概率,又称作 soft assignment 。
得出一个概率有很多好处,因为它的信息量比简单的一个结果要多,比如,我可以把这个概率转换为一个 score ,表示算法对自己得出的这个结果的把握。也许我可以对同一个任务,用多个方法得到结果,最后选取“把握”最大的那个结果;另一个很常见的方法是在诸如疾病诊断之类的场所,机器对于那些很容易分辨的情况(患病或者不患病的概率很高)可以自动区分,而对于那种很难分辨的情况,比如,49% 的概率患病,51% 的概率正常,如果仅仅简单地使用 50% 的阈值将患者诊断为“正常”的话,风险是非常大的,因此,在机器对自己的结果把握很小的情况下,会“拒绝发表评论”,而把这个任务留给有经验的医生去解决。
废话说了一堆,不过,在回到 GMM 之前,我们再稍微扯几句。我们知道,不管是机器还是人,学习的过程都可以看作是一种“归纳”的过程,在归纳的时候你需要有一些假设的前提条件,例如,当你被告知水里游的那个家伙是鱼之后,你使用“在同样的地方生活的是同一种东西”这类似的假设,归纳出“在水里游的都是鱼”这样一个结论。当然这个过程是完全“本能”的,如果不仔细去想,你也不会了解自己是怎样“认识鱼”的。另一个值得注意的地方是这样的假设并不总是完全正确的,甚至可以说总是会有这样那样的缺陷的,因此你有可能会把虾、龟、甚至是潜水员当做鱼。也许你觉得可以通过修改前提假设来解决这个问题,例如,基于“生活在同样的地方并且穿着同样衣服的是同一种东西”这个假设,你得出结论:在水里有并且身上长有鳞片的是鱼。可是这样还是有问题,因为有些没有长鳞片的鱼现在又被你排除在外了。
在这个问题上,机器学习面临着和人一样的问题,在机器学习中,一个学习算法也会有一个前提假设,这里被称作“归纳偏执 (bias)”(bias 这个英文词在机器学习和统计里还有其他许多的意思)。例如线性回归,目的是要找一个函数尽可能好地拟合给定的数据点,它的归纳偏执就是“满足要求的函数必须是线性函数”。一个没有归纳偏执的学习算法从某种意义上来说毫无用处,就像一个完全没有归纳能力的人一样,在第一次看到鱼的时候有人告诉他那是鱼,下次看到另一条鱼了,他并不知道那也是鱼,因为两条鱼总有一些地方不一样的,或者就算是同一条鱼,在河里不同的地方看到,或者只是看到的时间不一样,也会被他认为是不同的,因为他无法归纳,无法提取主要矛盾、忽略次要因素,只好要求所有的条件都完全一样──然而哲学家已经告诉过我们了:世界上不会有任何样东西是完全一样的,所以这个人即使是有无比强悍的记忆力,也绝学不到任何一点知识。
这个问题在机器学习中称作“过拟合 (Overfitting)”,例如前面的回归的问题,如果去掉“线性函数”这个归纳偏执,因为对于 N 个点,我们总是可以构造一个 N-1 次多项式函数,让它完美地穿过所有的这 N 个点,或者如果我用任何大于 N-1 次的多项式函数的话,我甚至可以构造出无穷多个满足条件的函数出来。如果假定特定领域里的问题所给定的数据个数总是有个上限的话,我可以取一个足够大的 N ,从而得到一个(或者无穷多个)“超级函数”,能够 fit 这个领域内所有的问题。然而这个(或者这无穷多个)“超级函数”有用吗?只要我们注意到学习的目的(通常)不是解释现有的事物,而是从中归纳出知识,并能应用到新的事物上,结果就显而易见了。
没有归纳偏执或者归纳偏执太宽泛会导致 Overfitting ,然而另一个极端──限制过大的归纳偏执也是有问题的:如果数据本身并不是线性的,强行用线性函数去做回归通常并不能得到好结果。难点正在于在这之间寻找一个平衡点。不过人在这里相对于(现在的)机器来说有一个很大的优势:人通常不会孤立地用某一个独立的系统和模型去处理问题,一个人每天都会从各个来源获取大量的信息,并且通过各种手段进行整合处理,归纳所得的所有知识最终得以统一地存储起来,并能有机地组合起来去解决特定的问题。这里的“有机”这个词很有意思,搞理论的人总能提出各种各样的模型,并且这些模型都有严格的理论基础保证能达到期望的目的,然而绝大多数模型都会有那么一些“参数”(例如 K-means 中的 k ),通常没有理论来说明参数取哪个值更好,而模型实际的效果却通常和参数是否取到最优值有很大的关系,我觉得,在这里“有机”不妨看作是所有模型的参数已经自动地取到了最优值。另外,虽然进展不大,但是人们也一直都期望在计算机领域也建立起一个统一的知识系统(例如语意网就是这样一个尝试)。
废话终于说完了,回到 GMM 。按照我们前面的讨论,作为一个流行的算法,GMM 肯定有它自己的一个相当体面的归纳偏执了。其实它的假设非常简单,顾名思义,Gaussian Mixture Model ,就是假设数据服从 Mixture Gaussian Distribution ,换句话说,数据可以看作是从数个 Gaussian Distribution 中生成出来的。实际上,我们在 K-means 和 K-medoids 两篇文章中用到的那个例子就是由三个 Gaussian 分布从随机选取出来的。实际上,从中心极限定理可以看出,Gaussian 分布(也叫做正态 (Normal) 分布)这个假设其实是比较合理的,除此之外,Gaussian 分布在计算上也有一些很好的性质,所以,虽然我们可以用不同的分布来随意地构造 XX Mixture Model ,但是还是 GMM 最为流行。另外,Mixture Model 本身其实也是可以变得任意复杂的,通过增加 Model 的个数,我们可以任意地逼近任何连续的概率密分布。
每个 GMM 由 $K$ 个 Gaussian 分布组成,每个 Gaussian 称为一个“Component”,这些 Component 线性加成在一起就组成了 GMM 的概率密度函数:
\[ \displaystyle \begin{aligned} p(x) & = \sum_{k=1}^K p(k)p(x|k) \\ & = \sum_{k=1}^K \pi_k \mathcal{N}(x|\mu_k, \Sigma_k) \end{aligned} \]根据上面的式子,如果我们要从 GMM 的分布中随机地取一个点的话,实际上可以分为两步:首先随机地在这 $K$ 个 Component 之中选一个,每个 Component 被选中的概率实际上就是它的系数 $\pi_k$ ,选中了 Component 之后,再单独地考虑从这个 Component 的分布中选取一个点就可以了──这里已经回到了普通的 Gaussian 分布,转化为了已知的问题。
那么如何用 GMM 来做 clustering 呢?其实很简单,现在我们有了数据,假定它们是由 GMM 生成出来的,那么我们只要根据数据推出 GMM 的概率分布来就可以了,然后 GMM 的 $K$ 个 Component 实际上就对应了 $K$ 个 cluster 了。根据数据来推算概率密度通常被称作 density estimation ,特别地,当我们在已知(或假定)了概率密度函数的形式,而要估计其中的参数的过程被称作“参数估计”。
现在假设我们有 $N$ 个数据点,并假设它们服从某个分布(记作 $p(x)$ ),现在要确定里面的一些参数的值,例如,在 GMM 中,我们就需要确定 $\pi_k$、$\mu_k$ 和 $\Sigma_k$ 这些参数。 我们的想法是,找到这样一组参数,它所确定的概率分布生成这些给定的数据点的概率最大,而这个概率实际上就等于 $\prod_{i=1}^N p(x_i)$ ,我们把这个乘积称作似然函数 (Likelihood Function)。通常单个点的概率都很小,许多很小的数字相乘起来在计算机里很容易造成浮点数下溢,因此我们通常会对其取对数,把乘积变成加和 $\sum_{i=1}^N \log p(x_i)$,得到 log-likelihood function 。接下来我们只要将这个函数最大化(通常的做法是求导并令导数等于零,然后解方程),亦即找到这样一组参数值,它让似然函数取得最大值,我们就认为这是最合适的参数,这样就完成了参数估计的过程。
下面让我们来看一看 GMM 的 log-likelihood function :
\[ \displaystyle \sum_{i=1}^N \log \left\{\sum_{k=1}^K \pi_k \mathcal{N}(x_i|\mu_k, \Sigma_k)\right\} \]由于在对数函数里面又有加和,我们没法直接用求导解方程的办法直接求得最大值。为了解决这个问题,我们采取之前从 GMM 中随机选点的办法:分成两步,实际上也就类似于 K-means 的两步。
- 估计数据由每个 Component 生成的概率(并不是每个 Component 被选中的概率):对于每个数据 $x_i$ 来说,它由第 $k$ 个 Component 生成的概率为
\[
\displaystyle
\gamma(i, k) = \frac{\pi_k \mathcal{N}(x_i|\mu_k, \Sigma_k)}{\sum_{j=1}^K \pi_j\mathcal{N}(x_i|\mu_j, \Sigma_j)}
\]
由于式子里的 $\mu_k$ 和 $\Sigma_k$ 也是需要我们估计的值,我们采用迭代法,在计算 $\gamma(i, k)$ 的时候我们假定 $\mu_k$ 和 $\Sigma_k$ 均已知,我们将取上一次迭代所得的值(或者初始值)。
- 估计每个 Component 的参数:现在我们假设上一步中得到的 $\gamma(i, k)$ 就是正确的“数据 $x_i$ 由 Component $k$ 生成的概率”,亦可以当做该 Component 在生成这个数据上所做的贡献,或者说,我们可以看作 $x_i$ 这个值其中有 $\gamma(i, k)x_i$ 这部分是由 Component $k$ 所生成的。集中考虑所有的数据点,现在实际上可以看作 Component 生成了 $\gamma(1, k)x_1, \ldots, \gamma(N, k)x_N$ 这些点。由于每个 Component 都是一个标准的 Gaussian 分布,可以很容易分布求出最大似然所对应的参数值:
\[
\displaystyle
\begin{aligned}
\mu_k & = \frac{1}{N_k}\sum_{i=1}^N\gamma(i, k)x_i \\
\Sigma_k & = \frac{1}{N_k}\sum_{i=1}^N\gamma(i,
k)(x_i-\mu_k)(x_i-\mu_k)^T
\end{aligned}
\]
其中 $N_k = \sum_{i=1}^N \gamma(i, k)$ ,并且 $\pi_k$ 也顺理成章地可以估计为 $N_k/N$ 。
- 重复迭代前面两步,直到似然函数的值收敛为止。
当然,上面给出的只是比较“直观”的解释,想看严格的推到过程的话,可以参考 Pattern Recognition and Machine Learning 这本书的第九章。有了实际的步骤,再实现起来就很简单了。Matlab 代码如下:
(Update 2012.07.03:如果你直接把下面的代码拿去运行了,碰到 covariance 矩阵 singular 的情况,可以参见这篇文章。)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 | function varargout = gmm(X, K_or_centroids) % ============================================================ % Expectation-Maximization iteration implementation of % Gaussian Mixture Model. % % PX = GMM(X, K_OR_CENTROIDS) % [PX MODEL] = GMM(X, K_OR_CENTROIDS) % % - X: N-by-D data matrix. % - K_OR_CENTROIDS: either K indicating the number of % components or a K-by-D matrix indicating the % choosing of the initial K centroids. % % - PX: N-by-K matrix indicating the probability of each % component generating each point. % - MODEL: a structure containing the parameters for a GMM: % MODEL.Miu: a K-by-D matrix. % MODEL.Sigma: a D-by-D-by-K matrix. % MODEL.Pi: a 1-by-K vector. % ============================================================ threshold = 1e-15; [N, D] = size(X); if isscalar(K_or_centroids) K = K_or_centroids; % randomly pick centroids rndp = randperm(N); centroids = X(rndp(1:K), :); else K = size(K_or_centroids, 1); centroids = K_or_centroids; end % initial values [pMiu pPi pSigma] = init_params(); Lprev = -inf; while true Px = calc_prob(); % new value for pGamma pGamma = Px .* repmat(pPi, N, 1); pGamma = pGamma ./ repmat(sum(pGamma, 2), 1, K); % new value for parameters of each Component Nk = sum(pGamma, 1); pMiu = diag(1./Nk) * pGamma' * X; pPi = Nk/N; for kk = 1:K Xshift = X-repmat(pMiu(kk, :), N, 1); pSigma(:, :, kk) = (Xshift' * ... (diag(pGamma(:, kk)) * Xshift)) / Nk(kk); end % check for convergence L = sum(log(Px*pPi')); if L-Lprev < threshold break; end Lprev = L; end if nargout == 1 varargout = {Px}; else model = []; model.Miu = pMiu; model.Sigma = pSigma; model.Pi = pPi; varargout = {Px, model}; end function [pMiu pPi pSigma] = init_params() pMiu = centroids; pPi = zeros(1, K); pSigma = zeros(D, D, K); % hard assign x to each centroids distmat = repmat(sum(X.*X, 2), 1, K) + ... repmat(sum(pMiu.*pMiu, 2)', N, 1) - ... 2*X*pMiu'; [dummy labels] = min(distmat, [], 2); for k=1:K Xk = X(labels == k, :); pPi(k) = size(Xk, 1)/N; pSigma(:, :, k) = cov(Xk); end end function Px = calc_prob() Px = zeros(N, K); for k = 1:K Xshift = X-repmat(pMiu(k, :), N, 1); inv_pSigma = inv(pSigma(:, :, k)); tmp = sum((Xshift*inv_pSigma) .* Xshift, 2); coef = (2*pi)^(-D/2) * sqrt(det(inv_pSigma)); Px(:, k) = coef * exp(-0.5*tmp); end end end |
函数返回的 Px 是一个 $N\times K$ 的矩阵,对于每一个 $x_i$ ,我们只要取该矩阵第 $i$ 行中最大的那个概率值所对应的那个 Component 为 $x_i$ 所属的 cluster 就可以实现一个完整的聚类方法了。对于最开始的那个例子,GMM 给出的结果如下:
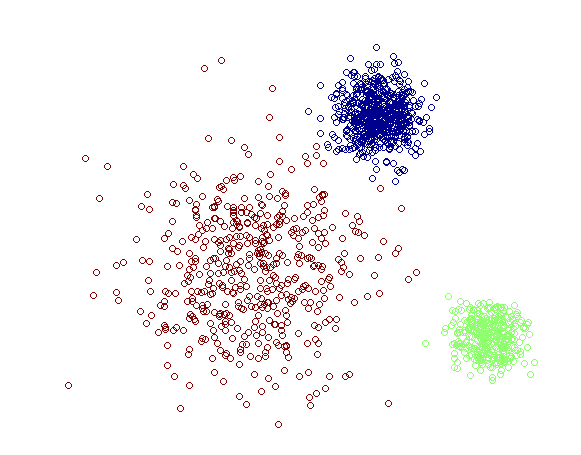
相对于之前 K-means 给出的结果,这里的结果更好一些,左下角的比较稀疏的那个 cluster 有一些点跑得比较远了。当然,因为这个问题原本就是完全有 Mixture Gaussian Distribution 生成的数据,GMM (如果能求得全局最优解的话)显然是可以对这个问题做到的最好的建模。
另外,从上面的分析中我们可以看到 GMM 和 K-means 的迭代求解法其实非常相似(都可以追溯到 EM 算法,下一次会详细介绍),因此也有和 K-means 同样的问题──并不能保证总是能取到全局最优,如果运气比较差,取到不好的初始值,就有可能得到很差的结果。对于 K-means 的情况,我们通常是重复一定次数然后取最好的结果,不过 GMM 每一次迭代的计算量比 K-means 要大许多,一个更流行的做法是先用 K-means (已经重复并取最优值了)得到一个粗略的结果,然后将其作为初值(只要将 K-means 所得的 centroids 传入 gmm 函数即可),再用 GMM 进行细致迭代。
如我们最开始所讨论的,GMM 所得的结果(Px)不仅仅是数据点的 label ,而包含了数据点标记为每个 label 的概率,很多时候这实际上是非常有用的信息。最后,需要指出的是,GMM 本身只是一个模型,我们这里给出的迭代的办法并不是唯一的求解方法。感兴趣的同学可以自行查找相关资料。

拜读了下,很不错
非常非常感谢,非常好
拜读了,非常感谢,非常非常透彻!!!
[…] K-means 和 GMM 这些聚类的方法是古代流行的算法的话,那么这次要讲的 Spectral Clustering […]
“那么我们只要根据数据推出 GMM 的概率分布来就可以了,然后 GMM 的 个K Component 实际上就对应了K 个 cluster 了”
对于任意形状的数据集,一个cluster或许并非单独一个component能够覆盖,这是GMM面临的关键问题了吧?
@clustering fancier
恩,GMM 就假设数据是 Gaussian 分布的,如果不是,可能效果就不好了,也可以采用多个 Gaussian 一起来表示一个 cluster ,或者采用非参数化的一些方法。
========================================================
Mixture Model 本身其实也是可以变得任意复杂的,通过增加 Model 的个数,我们可以任意地逼近任何连续的概率密分布。
========================================================
是不是意味着总可以找到一个GMM,能够任意逼近任何连续的概率分布,这样的话,即便数据不是高斯分布,效果也会不错?
@zhenming
理论上是的,但是模型越复杂,要“良好地” fit 该模型就需要越多的数据,然而,在实际中我们所拥有的数据总是有限的,所以实际中不可能这样盲目地通过增加模型复杂度的方法来解决问题,这通常会导致很严重的 Overfitting 。
拜读了,很透彻,谢谢
n个点,n-1阶的多项式就可拟合.
作者虽然写的是n阶,不过我估计也是n-1阶的意思.
@inzaghi250
嗯,失误了,确实是这样的,已经修正原文了,谢谢! 🙂
请问lz,聚类算法中不是事先并不知道数据要被聚成多少类的吗?我看lz的意思是聚类前就知道要聚成K类了。另外我的理解错误了,lz文中的K是需要计算的,应该怎么计算呢?期盼解答!!!
@小飞虾
你好,确定 K 正是聚类中一个非常困难的问题,大多数算法都要事先给定 K 的,通常也就根据对特定领域的先验知识取 K 或者一些实验方法来找甚至直接使用猜测的办法;此外,也有一些比较复杂的模型可以来确定 K 的,具体在实际中效果怎么样我也不是很清楚。
k-means 中的 k 可以用 bayesian information criterion 或 minimum description length 来估计吧
读了这篇文章,对聚类有了个初步了解,不过还是没有全部搞清楚,在找点资料吧。
hi,
代码注释中:
MODEL.Miu: a N-by-K matrix.
是不是应该是 N-by-D 阿.
嗯,对的,应该是 N-by-D ,谢谢指正!
呵呵, 你的文章非常清楚, 给我了很大启发, 该谢谢的人是我:)
楼主你好,为什么我的程序一直运行不正确?下面的warning,一直出不来结果?
Warning: Matrix is singular, close to singular or badly scaled.Results may be inaccurate. RCOND = NaN.
你好,如 warning 所说,矩阵出现奇异的情况,无法求逆了。
谢谢回复撒~~警告说矩阵接近是singular类型,大概意思是否是该矩阵数据比较单一,无法实现聚类?
我是把一幅图像直接作为输入的,不知道为啥会出现这种情况,楼主的输入数据是如何得到的呢?谢谢~~
你好,singular 是奇异的意思。参见 Wikipedia 。
⊙﹏⊙b汗,谢谢,我小菜鸟一个~呵呵
不过怎么才能保证一幅图像转化为矩阵后非奇异呢?这个程序不会只能针对非奇异矩阵吧?谢谢谢谢~~
我不是很明白你怎么把一幅图像转化为一个矩阵的,你不会就把图片当成一个矩阵了吧?建议你去了解一下机器学习方面的基础知识,比如《Pattern Classification》之类的书可以看一下。
额,一幅图像输入到MATLAB里,就是以矩阵的形式存储的~~
难道楼主不是把一幅图片以矩阵的形式存储的么?疑惑~~
楼主做图像方面的吗?
楼主写的特别号!但是我有一点没有看懂,第98行: coef = (2*pi)^(-D/2) * sqrt(det(inv_pSigma));第二个*是不是应该是除号吧,高斯分布的概率公式中,sqrt(det(inv_pSigma))是在分母上啊
因为已经求过逆了,所以就不要再用除号了呀。你说是不是?
sorry,我太不细心了!楼主的博客里关于机器学习的我大概都能用的上,我也是这个方向的,谢谢楼主啊。只不过我现在做的东西数据比较特殊,程序貌似用不上了,~~~~(>_<)~~~~
拜读了,写得通俗透彻,思路清晰。
楼主你好,我在Machine Learning中算是一个菜鸟级的人了,关于你的Gaussian Mixture Model我看了好长时间,因为我在尝试着做点实验,但是现在有关如何通过迭代方法获取r(i,k),我一点思路都没有,而且我是用自学的C#来做实验的,所以我很想了解这一步该如何实现,希望你能帮助我,谢谢!
你好,我想问一下,D维向量,K个component,Miu矩阵不是D*K矩阵么?
一样的啊,转置一下不就是 $K\times D$ 了吗?
不是,你那注释里面写的是N-by-D matrix,另外我想请教一个问题,如果我是利用GMM进行分类,每个类别建立一个GMM的话,我训练每个类别的GMM是就只用该类别的数据进行训练还是怎样比较好?我是新手,能否给点意见 谢谢~~
啊,确实是我写错了,已经更正了,谢谢。
GMM 是用来聚类的,当然你可以用 GMM 来为每一类数据建立一个模型,这样的话训练的时候也就是用那一类的数据来训练的。
嗯,好的,谢谢你,你的文章对我帮助很大~
深入浅出,比Ethem的ML那本书讲得好~
谢谢
深入浅出~
拜读了,谢谢
[…] by pluskid, on 2009-02-02, in Machine Learning 37 comments […]
[…] Gaussian Mixture Model 的迭代求解方法可以算是 EM 算法最典型的应用,而最开始说的 K-means […]
你好,我用你的方法使用一些样本点计算样本的概率密度函数p(x)。
1 我算得的Px中某点的值有的大于1了,这是正常的吗。我理解这是概率,Px所有元素值和为1?
2 我想用得到的GMM model计算新的样本点的概率密度值,是把px每一行直接相加吗?
你好,乘上每个 component 的权重,也就是 Pi 应该就不大于 1 了吧?相加之前记得要乘上权重。
没有,还是有的维度不对,总体之和也不为0.
难道是不能直接算概率密度函数?
谢谢你了
GMM 的 log-likelihood function 要对其进行最大化是可以通过求偏导硬推的,摆渡一下就好多推导过程了
写的很不错啊,简明扼要的讲解清楚了混合模型。EM算法在这儿虽然很方便,但是有一个问题就是singularity。 混合模型绝大部人其实是没有办法极大化似然函数的,特别是对指数族分布。
与 Amber 的提问相关:
GMM 是个概率密度函数,它在某个点上的值当然可能大于 1 !对概率密度函数做全积分,结果当然是 1 了。对某个实例(可以是向量),按 GMM(参数已估计好了的) 计算出某个分量的值,即使乘上其权值,也可能大于 1 的。
你好,我想请问下哪里可以找到您贴出来的这段程序?是哪个工具箱里面的吗
你好,这个是随便写的。不过 GMM 应该有很多工具箱,随便搜一下就能找到吧?
问个问题:在求协方差矩阵时,一般能否简化为求各维的方差,也就是假设协方差矩阵为对角线矩阵。这样运算量小些。盼回答!
有的时候是可以这样建模的,就是强制要求协方差是一个对角矩阵的情况,甚至还有强制要求协方差矩阵是对角阵并且元素全部相等的情况。这些时候通常是为了避免过拟合或者由其他一些先验知识而做的限制。
谢谢回答。再问一下:程序是否要对PX做一下归一化处理。你测试过每次PX求和是否近似为1吗?
[…] 以上步骤的Matlab代码(来自Free Mind)如下: function varargout = gmm(X, K_or_centroids) % ============================================================ % Expectation-Maximization iteration implementation of % Gaussian Mixture Model. % % PX = GMM(X, K_OR_CENTROIDS) % [PX MODEL] = GMM(X, K_OR_CENTROIDS) % % – X: N-by-D data matrix. % – K_OR_CENTROIDS: either K indicating the number of % components or a K-by-D matrix indicating the % choosing of the initial K centroids. % % – PX: N-by-K matrix indicating the probability of each % component generating each point. % – MODEL: a structure containing the parameters for a GMM: % MODEL.Miu: a K-by-D matrix. % MODEL.Sigma: a D-by-D-by-K matrix. % MODEL.Pi: a 1-by-K vector. % ============================================================ threshold = 1e-15; [N, D] = size(X); if isscalar(K_or_centroids) K = K_or_centroids; % randomly pick centroids rndp = randperm(N); centroids = X(rndp(1:K), :); else K = size(K_or_centroids, 1); centroids = K_or_centroids; end % initial values [pMiu pPi pSigma] = init_params(); Lprev = -inf; while true Px = calc_prob(); % new value for pGamma pGamma = Px .* repmat(pPi, N, 1); pGamma = pGamma ./ repmat(sum(pGamma, 2), 1, K); % new value for parameters of each Component Nk = sum(pGamma, 1); pMiu = diag(1./Nk) * pGamma' * X; pPi = Nk/N; for kk = 1:K Xshift = X-repmat(pMiu(kk, :), N, 1); pSigma(:, :, kk) = (Xshift' * … (diag(pGamma(:, kk)) * Xshift)) / Nk(kk); end % check for convergence L = sum(log(Px*pPi')); if L-Lprev < threshold break; end Lprev = L; end if nargout == 1 varargout = {Px}; else model = []; model.Miu = pMiu; model.Sigma = pSigma; model.Pi = pPi; varargout = {Px, model}; end function [pMiu pPi pSigma] = init_params() pMiu = centroids; pPi = zeros(1, K); pSigma = zeros(D, D, K); % hard assign x to each centroids distmat = repmat(sum(X.*X, 2), 1, K) + … repmat(sum(pMiu.*pMiu, 2)', N, 1) – … 2*X*pMiu'; [dummy labels] = min(distmat, [], 2); for k=1:K Xk = X(labels == k, :); pPi(k) = size(Xk, 1)/N; pSigma(:, :, k) = cov(Xk); end end function Px = calc_prob() Px = zeros(N, K); for k = 1:K Xshift = X-repmat(pMiu(k, :), N, 1); inv_pSigma = inv(pSigma(:, :, k)); tmp = sum((Xshift*inv_pSigma) .* Xshift, 2); coef = (2*pi)^(-D/2) * sqrt(det(inv_pSigma)); Px(:, k) = coef * exp(-0.5*tmp); end end end […]
学些了. 写的很不错,浅显易懂.
写的非常好,非常感谢。虽然大体读了一下,还没太懂,还需要再仔细研究一下~^_^
想问一下,你一般做实验用什么数据集,是自己生成还是现实的标准数据集?
用标准数据集。
哪个标准数据集?推荐一下
这取决于你要做什么实验啊。如果你要做哪一方面的工作,找相关领域的前人的论文来看就知道哪些是经常用到的,就是标准数据集了。
可否这样认为GMM与K-means的区别:GMM在更新的时候某个分布的参数时所有的数据点都对这个分布有影响,只是对于这个分布概率小的点贡献也小,而k-means在求新的中心的时候,并不是所有的点都对新的这个中心有贡献,只是那些与上一步的中心近的点才有所贡献
嗯,可以这么说,虽然 K-means 和 GMM 之间的区别还有其他一些地方。
还有其他一些地方? 如有闲暇,还望指教!
“尽可能好地拟核给定的数据点”
拟核 -> 拟合
恩, GMM 跟 Fourier Transform 有异曲同工之妙…
updated 🙂
lz文中提到,高斯分布具有良好的计算特性,请问主要有哪些特性呢。另外对于各种混合模型,我们为什么通常选择GMM呢?谢谢赐教。
Lz文中提到,高斯分布具有良好的计算特性,请问主要有哪些特性呢。另外对于各种混合模型,我们为什么通常选择GMM呢?谢谢赐教。
你好,Gaussian Distribution 算是最简单的一种分布啦,好的性质,比如说两个 Gaussian 相乘还是 Gaussian 。当然,这个其实是 exponetial family 所共有的特征。你好,后面由网友指出来了,我这里犯了一个很严重的错误:高斯分布的乘积并不是高斯分布。
不过它仍然有其他比较好的性质,比如在平面上,要将两个高斯分布的数据类别分开来的最优的分界线是二次曲线,如果两个分布的 variance 是一样的话,还可以变成简单的直线。高维情况下是类似的。另外,已知数据点之后来估计高斯分布的参数也是比较简单的。
who told you that the product of two normal distritubtions is till normal?
Sorry I made a serious mistake here. Thanks for pointing out this.
两个Gaussian分布相加应该是Gaussian分布。您说的“在平面上,要将两个高斯分布的数据类别分开来的最优的分界线是二次曲线,如果两个分布的 variance 是一样的话,还可以变成简单的直线。”这一性质,我到没见过,没有太大的概念。是不是应该在数值分析后可以显示出来?
就是两个 Gaussian 相减等于零(就是分隔的那个曲线/面),这个解析式是一个二次的,印象中《Pattern Classification》好像有详细分析三维中的各种情况的。
soft assignment 和GMM 应该不是完全相等吧,他们有什么区别和联系呢?
我想知道K值如何估算?还有πk 如何估算?我是初学者~请指点,谢谢
你好,传统的 GMM 算法无法估计 k ,需要实现给定的。
那么,先用k-mean确定所有的初值在进一步迭代可以吧?
嗯,可以的。
师兄研二啊,今年?
假设我有一批数据,希望用GMM进行拟合,那么我该如何操作?这个K的给定有什么方法或者技巧?非常感谢
根据先验知识来定,或者枚举找最优的吧。也有方法可以自动估计类别数目的,比如 Data Spectroscopy: Learning Mixture Models using Eigenspaces of Convolution Operators 。不过没有尝试过,不知道在实际数据上效果如何。
我又在文献中看到过hold-out方法,就是枚举吧?从K=1开始,一直到K=n+1时过拟合就停止,将K=n视为optimal,是不是可以?
还有如果是用K-mean的结果作为初值,那么k-mean聚类出的cluster数目是不是可以作为K的初值?然后其他的参数一并计算?
kmeans 本身也是需要预先指定 k 的取值的
[…] overfit 和 underfit 的问题可以参见这篇文章的 3~6 段,这位学长讲得非常深入浅出了。课上提到的一种解决方法叫 […]
lz,请问:为了决定最优的K值,我先用K-mean,从K=1开始进行聚类,然后K+1……依次进行下去,直到K+1时的J大于K时的J,即过拟合,就停止,选取此时的K作为GMM的K,可以么?
你的 J 是 kmeans 的目标函数吗?如果是那样的话,是行不通的,因为 kmeans 的目标函数肯定随着 k 增大而减小,当 k 等于数据点个数的时候 J = 0 。如果想要自动确定 GMM 类别个数的话,确实是有一些工作的,比如 Belkin 的 Data Spectroscopy: Learning Mixture Models using Eigenspaces of Convolution Operators 这个工作。实际我没有试过,不知道在实际数据中效果如何。
那该怎么确定GMM的类别个数啊?
还有一个疑问,这个GMM做出来的应该是连续的,而且它的每个部分也是连续的;那么你在找最优的参数的时候,怎么能计算一个点的概率?不是没有意义么?
辛苦楼主~
我按照你的代码执行了一遍,为什么这个矩阵Px里面有的值大小超过了1?这个是可以的??
你好,Px 只是把数据点 x 带入到 Gaussian model 里得到的值,可以超过 1 的。
lz,假设一下:一堆状态点,每个点是一个三维的数据,我用了GMM建模,找到了其联合pdf;现在我有一个新的状态点,我要求它的概率,显然单点的是没有意义的,而且在小区域内的概率也是很小的吧,那么这个除了将点归类还有什么其他的意义?这个问题对我来说很棘手,请楼主原谅问题的愚蠢~谢谢~~·
你好,不好意思,我不太明白你想要解决的问题是什么,或者你想要做什么。
你好,我现在在写ICP方面的论文,看到Gaussian Mixture Models后,感觉可以在这方面下手,提出一种新的方法,请问,您能给出解决散文点云空间分布的高斯混合模型的C++代码吗?非常感谢!!
我是想求某个状态点的概率
像 Gaussian 分布这种绝对连续分布单点的概率是为零的。
我知道……您见我的邮件吧……我实在描述不清楚了,麻烦您了
非常棒的文章。
另外BOA就相当于美国的建行 : D
我们实验室也好几个浙大的师兄,都是非常棒,祝贺楼主拿到MIT的offer(我是不是回错地方了,不过这两天一直琢磨您这篇文章来的,快考试了= =|||)
能否推荐两本讲聚类算法或模式识别方面较经典的书籍?!谢谢!
你好,《Pattern Classification》挺不错的。
文章很强大
受教
转载一下,谢谢!
如不宜,请email通知我。
师兄好,能否给解释一下高斯模型公式中T是指的什么?就是exp的次幂里的那个T
你好,T 是矩阵转置。
师“熊”的文章果然好强大!!看了确实受益匪浅……我依然有两个小问题不明:
1)我学的是用混合高斯模型对背景建模方面的,假设一个像素点与模型第一次匹配成功后,就可以说这个像素点是背景点了,那么还要继续和后面的(2至4个)模型匹配吗?
2)更新后权值怎么保证累加和为1呢?或者说权值累加和必须要等于1吗?
3)alpha的值是自己设定的经验值吗?大概为多少?
跪谢!!!
师兄,请问在matlab运行到第96行( inv_pSigma = inv(pSigma(:, :, k));)时,警告说矩阵奇异,为什么会出现这种情况啊?按道理来说,对于聚类的数据应该是没有特殊要求的啊!
非常感谢!!打扰了!
你好,这个 code 主要是 demo code ,为了结构清晰很多地方没有做细致处理,例如那里求逆的时候我们一般是不会直接用 inv 来求的,可以用 \ 或者 / 直接来解方程。另外这里也没有对 covariance 做任何限制或者 regularization ,如果数据量不够多的话这是不好的并且很可能出现你说的这种情况。所以,如果你是想跑实验的话,最好是去找网上其他专门写来跑实验的 GMM 代码,不仅处理了各种情况,而且速度也会快许多。 🙂
麻烦师兄给个程序……我没找到啊……谢谢了
哈哈,还是kid的blog好
文章太强大了,看不太懂呢!师兄,恕我无知,你那个程序运行出来的结果varargout应该是什么样的矩阵?我想输入一幅高清图像的灰度值矩阵,为21025*200的矩阵,给其分15类,但貌似总是运行不了,学长能解释一下吗?还有,第83行 [dummy labels] = min(distmat, [], 2)中的dummy是做什么用的,貌似出错。。。
dummy 是无用的变量。
代码中将每个数据点看做是D维的,如果将NxD数据替换为一幅图像,可以直接用吗? % new value for pGamma
pGamma = Px .* repmat(pPi, N, 1);
pGamma = pGamma ./ repmat(sum(pGamma, 2), 1, K);
第一行中pGamma 不已经是概率了吗?为什么还要第二行?请教一下!先谢了
正好读了下,楼主分析的很好很强大~顺便回答下这位童鞋
第一行是求的step 1中公式的分子,还没有计算完;第二行是除以公式中的分母,结果才是 soft membership~ lol~
那么GMM是计算将数据点assign到某个类别的概率,这个作用和FCM模糊聚类有什么差异?
[…] 我之前写过一篇介绍 Gaussian Mixture Model (GMM) 的文章,并在文章里贴了一段 GMM 实现的 Matlab 示例代码,然后就不断地有人来问我关于那段代码的问题,问得最多的就是大家经常发现在跑那段代码的时候估计出来的 Covariance Matrix 是 singular 的,所以在第 96 行求逆的时候会挂掉。这是今天要介绍的主要话题,我会讲得罗嗦一点,把关于那篇文章我被问到的一些其他问题也都提到一下,不过,在步入正题之前,不妨先来小小地闲扯一下。 […]
[…] a comment » 我之前写过一篇介绍 Gaussian Mixture Model (GMM) 的文章,并在文章里贴了一段 GMM 实现的 Matlab […]
[…] 如果说 K-means 和 GMM 这些聚类的方法是古代流行的算法的话,那么这次要讲的 Spectral Clustering 就可以算是现代流行的算法了,中文通常称为“谱聚类”。由于使用的矩阵的细微差别,谱聚类实际上可以说是一“类”算法。 […]
你好:请教一个问题,多维的数据,如何可视化聚类结果!就是上面那个图是怎么画的?
第三次来看这篇文章,前两次看了不太明白,回去查了不少资料,今天终于全明白了…感谢楼主~!
你好,小弟今天發現您的blog,拜讀了這一整個系列的文章,以及其他許多,受益良多。很少遇到像你這樣能夠把數學解釋的清楚透徹並且附上source code的,無論是python or matlab,把source code實際載下來玩能夠更深刻地體會抽象的演算法,非常感謝您無私的分享,學習了 lol。
师兄,您好,我是研一的新生,您的这篇文章我已经看了好久了,并且基于你的这篇文章的代码,重新编写了一些代码,也是关于高斯混合模型的,只不过是将每一个component看成是由一个高斯混合模型组成的,也就是将原先的高斯分布假设成了高斯混合分布,
然后就是在求高斯分布时的协方差矩阵求逆时会出现奇异的情况,不知道师兄可否给点建议,鄙人将不甚感激~
你是说,两层的混合高斯模型?这个和普通的混合高斯模型不是一样的吗?
如果使用EM-MAP聚类的话,一个先验假设是每个component具有相同的权值,也就是Mixture里面那个alpha,这个假设是不是有点arbitrary,不知道之前有没有人做过优化这个权值的工作呢?
师兄说的两层高斯混合模型就是把类用高斯混合模型拟合吧,原先高斯模型是用高斯分布拟合的,应该就是我做的模型,我是基于半监督学习上的高斯混合模型分类,函数输进去的是已知数据的先验概率和各类高斯混合模型的中心点坐标。更新的值是先验概率和中心点坐标的值,采取迭代的方式,不知道是我代码出错还是有什么限制,分出的图像效果不好,望师兄指点。
我不是很清楚你是在做什么,就是每个类别分别 train 出 GMM ,然后分类的时候看每个类别的似然?GMM 的 covariance singular 的话,可以加 regularization,具体可以看我这篇 blog : http://freemind.pluskid.org/machine-learning/regularized-gaussian-covariance-estimation/ 。分类效果不好的话,这个可能有很多因素,我也不知道了呀。
师兄真是热心人……
厉害!
为什么第k个协方差矩阵是pSigma(:, :, k)而不是pSigma(k, :,:),这样做有什么好处?
在 matlab 里 (:,:,k) 是个矩阵,(k,:,:) 是个 tensor,需要 squeeze 一下才行
您好,用pinv代替inv是不是就能处理pSigma不可逆的情况?
你好,应该是可以解决计算的问题,它忽略掉那些零的特征值进行求逆的话,应该也可以从某种角度来进行 regularization 的解释,不过 pinv 计算开销挺大的。
你好,看了你的文章收获很大啊,很牛!!!但是我还有个问题想问一下,高斯混合模型中的各个component之间是否相互独立呢?
你好,给定属于哪个 component 之后,各个 component 是相互独立的。
那能不能把每个component 合成一个正态分布呢?
什么意思?每个 component 不本来就是正太分布吗?
不是独立正态分布相加还是正态分布吗,那这些component相加应该还是一个正态分布?不知道我这样理解可不可以
“两个正太分布随机变量的和”和“两个正太分布概率密度函数的和”是不同的东西。
哦,看样子,还有些概念没弄清楚,谢谢指导啊,我再琢磨一下
Excellent!博主,请多谢文章,受益匪浅!!
博主,该怎么将结果绘图出来了?
matlab scatter 可以画。
急求回复,博主,谢谢,谢谢!!
博主,那怎么讲一个1000个点的坐标值转为N*D的X矩阵呀?我现在的数据是2*1000的矩阵。
lz,如何求解一维混合高斯分布的极值(点)?谢谢!
很好的东西,讲得很透彻。
在code的注释中,
MODEL.Miu: a K-by-D matrix
如果用一个D-by-K matrix,本质上是一样的,但物理意义上是否和另外两个参数更一致些?
如果使用EM-MAP聚类的话,一个先验假设是每个component具有相同的权值,也就是Mixture里面那个alpha,这个假设是不是有点arbitrary,不知道之前有没有人做过优化这个权值的工作呢?
或者也许是这个问题不太重要?
可以用 kmeans 来初始化。
你好
程式碼中的
coef = (2*pi)^(-D/2) * sqrt(det(inv_pSigma));
det(inv_pSigma)是不是要用pSigma而不是inv_pSigma?
感謝
inv_pSigma 没有错吧,因为那个东西是在分母上的。
求问函数最后返回的时候 varargout = {Px, model}为什么是Px而不是 pGamma?
Px应该只是高斯函数的值,pGamma才是后验概率啊。。。
输出参数的后验概率来做什么?求的是数据的概率呀。当然你想要的话也可以输出来没有什么关系……
不好意思是我弄错了- -。。。应该是比较数据点x属于各个特定分布的概率来决定x属于哪个簇,而不是求x由该分布生成的概率,多谢~
不好意思,可能是我才疏学浅,仔细想想还是无法理解。。。《Pattern Recognition and Machine Learning》的9.3.2讲与K-means的关系的时候,第一段说“makes a soft assignment based on the posterior probabilities”,这个soft assignment应该就是r(z_{n,k}),也就是数据点被 assign 到每个 cluster 的后验概率啊。。。而K-means中数据点的hard ssignment也是根据r(z_{n,k})的极限值得到的,为什么这里不是根据比较r(z_{n,k})的大小来确定数据x属于哪个簇呢?
哦,我明白你的意思了。两者的区别是 P(x|k) 和 P(k|x),最后归为 hard decision 的时候可以看成分别是 ML 和 MAP 两种方法,各自也是有道理的,不过如果要和 PRML 上的一致的话,应该确实是用你说的这种 MAP 做 hard decision 的~
明白啦,感谢~
tmp = sum((Xshift*inv_pSigma) .* Xshift, 2);
这里是不是漏掉一个转置符号,在前一个Xshift上?
转置以后维度就不对了。
文章不错,赞一个,但是程序中
distmat = repmat(sum(X.*X, 2), 1, K) + …
repmat(sum(pMiu.*pMiu, 2)’, N, 1) – …
2*X*pMiu’;
[dummy labels] = min(distmat, [], 2);
for k=1:K
Xk = X(labels == k, :);
不懂,跪求解答!
我想问一下,混合高斯模型与多个服从正态分布的随机向量线性组合之间有什么关系?
基本上没有什么关系吧。
您好!现在正看GMM,您的文章让我受益匪浅,感谢您的分享,谢谢。
你好,我在测试数据时候,遇到问题是矩阵本身不是奇异的,但是对角矩阵的对角元比较小例如0.003,d较大(超过100)的时候matlab处理精度不够运行出来det(covMatrix)=0,我加了缩放因子之后得到的likelyhood就特别大,是处理方式上有问题吗?谢谢指教
楼主,看了你的帖子我明白了GMM 的实现过程受益匪浅,请问楼主如果我想检测图像中的异常行为,首先我提取了正常行为的特征信息,然后用GMM为正常行为的特征空间建立模型。但是,检测时我有遇到问题,按照我的想法是将被测特征向量输入到训练好的GMM中,希望能得到一个概率,如果这个概率小于某个阈值它就不是正常行为,可是,我这里属于被测特征后,得到值非常大,请问楼主我该怎么应用GMM才可达到我预期的目的的(就是希望GMM能给出关于被测点的一个概率,然后,通过这个概率进行判断),当然我的数据属于离散的,因为针对的是图像,希望楼主给予答复十分感谢。
你好,GMM 是连续型的概率分布,所以你不会得到一个 0 到 1 之间的概率值。我觉得你需要同时搜集正常数据和异常数据然后根据这些数据决定出一个合理的阈值出来,或者你也可以正常和异常各训练一个模型然后比较概率(密度)大小。
你好,我也是用这个做图像的,能不能交流一下的?
这个程序我怎么的实现不了的,在的matlab上不能运行的?
im=imread(‘img1.jpg’);
im1=rgb2gray(im);
imshow(im1)
varargout = gmm(im1, 2);
不能调用的,谢谢了,我是菜鸟的,不要见笑
博主,你好。你写的这个关于EM算法的博文很好很强大。我用你的MATLAB代码跑了下数据。发现,最后算出来,每个数据的最后的概率都很低啊,10^(-5)数量级的概率值都算大的了。请问这个正常么?我感觉从道理上讲不通啊,我即便讲训练出来的均值代入训练好的模型,计算出来的概率也很小啊。
连续型随机变量得到的是概率密度并不是概率值。
我的意思是,概率密度函数是最后训练出来的模型啊,就是混合高斯模型中,每component的协方差矩阵和期望,以及每个component对应的概率pi.有了这个模型后,将一个数据X代入这个模型,对于每个component都会算出一个对应的概率,然后这个概率乘以相应的pi,最求就和,就是这个数据X,在这个混合模型下,算出的概率啊。我的理解不对么??代码跑完,最后结果的PX,不就是所有训练数据X在各个component下的概率么?看起来都非常小啊。
那个是概率密度值,不是概率。如果你一定要算概率,连续型随机变量下单点的概率是零。如果你要算一个区域的概率,可以针对概率密度进行积分。
另外,博主,我觉得你给出的公式有问题,你在文中提到:
估计数据由每个 Component 生成的概率(并不是每个 Component 被选中的概率):对于每个数据 来说,它由第 个 Component 生成的概率是Gamma(Xi,k)…根据EM算法原理和你给出公式的右边,我觉得应该是Gamma(k=j|Xi)
Gamma 是个普通的函数,你这样改变形式的记号没有什么区别吧。
哦,原来博主您只是将Gamma表示为一个普通的二元函数啊,我以为你的意思是表示的概率密度函数,所以我就理解为联合概率密度函数,我就觉得右边不对啊,原来是这样啊。
你好,博主可以请问一下特征矩阵怎么做?我是学生物的,外行。想给行为数据分类,我还有标签但具体不知道怎么标上去,书都好虚,具体怎么匹配特征矩阵怎么训练?我都是用R做的,如果有R代码就更好了。一直找不见。
哦,对的,明白了。感谢博主的耐心解答。
另外,在请教博住一个问题。就是我看到很多资料都说用EM算法,比如估计GMM的参数,最后得到的都是局部最优解。我不理解的是,从EM算法的形式上看,优化的目标函数是凹函数,求最大化目标函数的解,这是个凹问题,应该有全局最优解啊,为何最后求解出来的只是局部最优解?
因为对两组变量分别 convex 并不代表一定 jointly convex,这里就是这种情况。
呃~~,博主能稍微说具体点么?是哪两个变量呢?另外,个人愚见,总觉得,最后的优化函数是LOG函数,总是凹函数,应该最后结果总应该是全局最优吧~~
博主你好,我也是浙大的研究生,我现在在做无线传感执行网方面的研究。我现在遇到一个问题,想请教一你。在上面的例子中,数据是二维的,服从一个二维正态分布,即离中心点越近,点就越稠密。如果我有一组数据,是三维的,也是服从正态分布:z=f(x,y),其中f是二维正态分布的pdf,那么通过一组三维数据(x,y,z),该如何利用GMM来估计它的均值和方差呢?
你好,我听你的描述似乎问题和 GMM 没有什么关系啊,如果你知道是服从正态分布的话,那么直接进行正态分布的参数估计应该就可以了吧?
你好,想进一步请教一下你说的GMM的偏执问题,好比一个语音识别,里面有3类声音(男声,女声,机器声),按照你说的GMM的偏执,认为这3类声音的数据分布就是3个正态分布的叠加(为什么有这样的结论?),那是不是也有这样的结论每一类声音就是一个正态分布,那其实所有的GMM就可以转化为数个SGM,那这样求解也就不需要什么EM算法了,直接求最大似然函数就可以了?
你好,GMM 的最大似然目标函数不是 convex 的,其实 EM 算法就是一种迭代的求解这个最大似然目标函数的一个局部最优解的算法。
你好 我想請問一下初始參數中的pMiu是什麼,以及這三個初始參數該如何設定 是可以任意設嗎
pMiu 就是文章里的 \mu,初始值可以任意设定,会得到不同的 local optimal solution
我想问一下如何评价GMM的聚类效果,因为GMM跟K-Means不一样,GMM只是给出了每一个样本属于各个Gaussian的概率,而K-Means是严格的给出了这个样本属于某个类。GMM这个可以用跟K-Means一样最常用的正负类聚类评价方式吗?
只要根据 GMM 的概率密度值去最大的进行 hard assignment 得到聚类结果就可以和 k-means 类似地进行评价。
博主,还想请教您一下,我还是有些不大明白。就比如我想用聚类准确率
P=TP/TP+FP这个公式来评价聚类精度,其中TP是指属于正类并被划分到正类的样本
数,FP是指属于负类但被划分到正类的样本数。我想问一下GMM中如何统计TP的个
数,也就是TP在GMM中代表什么,是代表每一个样本被划分到各个Gaussian模型的
最大概率个数吗?也就是说GMM给出该个样本属于某个Gaussian的概率超过50%我
就认为该样本聚类正确?还是怎么?比如,我有1000个样本,分到1O个GMM中,或者分到20个GMM中,都会给出每个样本属于各个GMM的概率,有的样本的概率超过50%,有的低于50%,是不是超过50%就认为聚类准确?还是什么
博主,还想请教您一下,我还是有些不大明白。就比如我想用聚类准确率P=TP/TP+FP这个公式来评价聚类精度,其中TP是指属于正类并被划分到正类的样本数,FP是指属于负类但被划分到正类的样本数。我想问一下GMM中如何统计TP的个数,也就是TP在GMM中代表什么,是代表每一个样本被划分到各个Gaussian模型的最大概率个数吗?也就是说GMM给出该个样本属于某个Gaussian的概率超过50%我就认为该样本聚类正确?还是怎么?比如,我有1000个样本,分到1O个GMM中,或者分到20个GMM中,都会给出每个样本属于各个GMM的概率,有的样本的概率超过50%,有的低于50%,是不是超过50%就认为聚类准确?还是什么
你好,关于聚类的 evaluation,可以看 k-medoids 那篇里的末尾有提到一点:/?p=40
coef = (2*pi)^(-D/2) * sqrt(det(inv_pSigma));这个有问题吧。
另外对于奇异的协方差矩阵,求逆会出问题,这个怎么解决比较好,用pseudo-inverse?
协方差 singular 的时候可以加 regularization,参见这篇文章: http://freemind.pluskid.org/machine-learning/regularized-gaussian-covariance-estimation/ (其实文中已经写了协方差奇异会出现问题并且给过这个链接了……)
[…] Gaussian Mixture Model 的迭代求解方法可以算是 EM 算法最典型的应用,而最开始说的 K-means […]
[…] 得出一个概率有很多好处,因为它的信息量比简单的一个结果要多,比如,我可以把这个概率转换为一个 score ,表示算法对自己得出的这个结果的把握,参考pluskid大神博文 […]
[…] 主要参考资料: 《Pattern Recognization and Machine Learning》 帮助理解: /?p=39 […]
>> gmm(X, K_or_centroids)
Undefined function or variable ‘X’.
这个X怎么定义?
我理解X就是数据集合,这个可以从实验中得出,或者就是实际分布的数据。例如图像的灰度级,对应着直方图(一种概率密度函数),这里的X就是这些灰度级,一般是0-255
请教博主,程序中只使用了数据点X,都没有提到这些数据点X对应的真实的概率密度函数,通过E-M算法得到的参数pMiu,pPi,pSigma后,对应的GMM和实际的概率密度函数的关系没有提及到。其实我有一个简单的想法,能否假设有pMiu,pPi,pSigma组成了拟合成其中一个Px,将这个Px和真实的概率密度函数,假设为hx,求Px和hx的均方差,设此均方差为目标函数,使目标函数最小。使用一些全局最优算法来求得pMiu等参数呢?
博主,你的训练数据是由 Mixture Gaussian Distribution 生成的数据,具体怎么实现的啊,怎么从这个混合分布模型中产生随机点啊,我也生成这些点,能提供一份代码吗
请教博主,有几个问题
1.在做GMM之前需要对样本数据进行分析么,看看是否可以用GMM, 如何做?
2.在数据进入GMM前,对数据处理的工作有哪些?标准化?
3.离散、连续混合特征可以做GMM么
多谢博主,才看了个开头,就吸引住了。
同一个分布,在同等k下,可以有多个一簇Gauss分布
[…] 漫谈 Clustering (3): Gaussian Mixture Model […]
博主,如果使用一些数据训练GMM,去分类另一些数据,是不是要求所有数据的种类比例相近?例如训练集每组数据都是10个男生,1个女生;测试集都是1个男生,10个女生,这种情况能用GMM吗?