机器学习物语(4)：PAC Learnability

这次我们要介绍的话题是 PAC Learnability ，直译过来就是 PAC 可学习性。可学习性听起来和计算理论里的可计算性是很类似的，当然其实也确实是类似的，而且这里也包含一些计算理论里的内容。对比来看，这里研究的主要是三个问题：

• 计算理论研究什么时候一个问题是可被计算的，而 PAC 学习理论，或者说计算学习理论 (Computational Learning Theory) 主要研究的是什么时候一个问题是可被学习的。可计算性在计算理论中已经有定义，而可学习性正是我们待会要定义的内容。
• 另外，计算理论中还有很大一部分精力花在研究问题是可计算的时候，其复杂度又是什么样的，因此，类似的，在计算学习理论中，也有研究可学习的问题的复杂度的内容，主要是样本复杂度 (Sample Complexity) 。
• 最后，在可计算的时候，得到实现计算的具体算法也是计算理论中的一个重要部分；而学习理论（或者更多的在“机器学习”这个课题下）当然也会探讨针对可学习的问题的具体的学习算法。

而 PAC 模型在这里的作用相当于提供了一套严格的形式化语言来陈述以及刻画这里所提及的 Learnability 以及 (Sample) Complexity 问题。

虽然也可以扩展用于描述回归以及多分类等问题，不过最初的 PAC 模型是针对 binary classification 问题提出来的，我们这里也采用这种模型，并且可以顺便介绍这种情况下的一些特有的概念。和以前的设定类似，我们有一个输入空间 $X$ ，也称作 Instance Space 。$X$ 上的一个概念 $c$ 是 $X$ 的一个子集，或者用之前用过的语言来说，$c$ 是从 $X$ 到 $\{0,1\}$ 的函数，显然，$c$ 可以用所有函数值等于 1 的那些点 $c^{-1}(1)$ 来刻画，那些点构成 $X$ 的一个子集，并且“子集”和“函数”在这里是一一对应的，于是我们将两个概念直接等同起来。用集合的语言来描述 binary function 的好处是可以用集合操作来对函数进行操作。比如，假设 $h$ 是另一个 $X$ 上的 binary function ，假设我们试图用 $h$ 去逼近 $c$，我们选择 $X$ 上的一个概率分布 $\mu$ ，则根据以往关于误差（或者风险）的定义，我们有 $\mathcal{E}(h) = \mu(h(X)\neq c(X))$ ，而这个量可以很容易并且很直观第用集合的对称差来表示：

\[
\mathcal{E}(h) = \mu(h\Delta c)
\]

如图所示，误差在这里就很直观地用两个集合的对称差（也就是黄色的部分）的面积（用测度 $\mu$ 衡量）了：

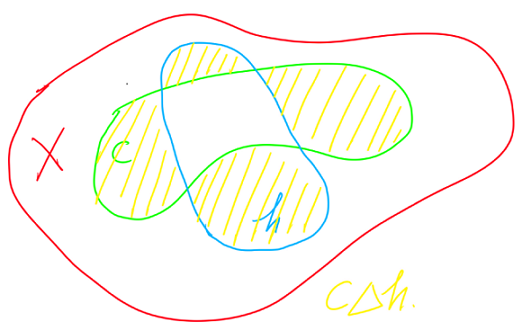
$X$ 上的一个 concept class $\mathcal{C}$ 就是一堆这样的 concept 的集合，也就是 $X$ 的 power set 的一个子集。这里的 $\mathcal{C}$ 也就对应之前的设定中的函数空间 $\mathcal{F}$ 。类似的，学习问题实际上就是给定一个 target concept $c\in\mathcal{C}$ ，寻找一个逼近 $h\in\mathcal{C}$ 的问题。

对比之前的统计学习的设定，可以发现一些差异，比如这里的 target concept 是一个确定的函数，也就是说，对应 $x$ 的 $y$ 是取一个固定的值，而不是一个随机变量；更严重的是，这里 target concept $c$ 是属于学习用的 concept class $\mathcal{C}$ 里面的，因此理论上是能达到 0 误差的。不过虽然最初基本的 PAC 学习的一些结果是在这样的框架下得到的，但是我们这里的重点是要给出 PAC Learnability 的定义，在这种情况下，这些限制都是可以放松和扩展的，我们待会再会过来看这些问题。

“计算学习理论”顾名思义会考虑“计算”在里面，因此，和普通的统计学习理论中所考虑的设定——事先给定了一个训练数据集——所不一样的是，我们这里并不给定一个数据集，而是给定一个可以生成数据集的 procedure $EX(c,\mu)$ ，也称 oracle ，每次调用可以 IID 第从 $\mu$ 里采样一个 $x$ ，并返回 $(x,c(x))$ ，不妨假设 $EX(c,\mu)$ 的运行（计算）时间是单位时间。下面我们来看一下我们理想中的学习算法应该满足一些什么条件

• 首先对 $EX(c,\mu)$ 的调用次数应该不要太多
• 然后算法的计算量（包括对 $EX(c,\mu)$ 以及本身的其他运算）不要太大
• 算法能够得到一个误差足够小的 $h\in\mathcal{C}$

至于什么是“太大”或者“太多”呢？我们下面就给出严格的定义

下面我们来细看一下这个定义，这里重要的两个参数，一个是 $\epsilon$ ，用来限制模型的误差，但是，由于学习到的模型是依赖于（通过 $EX(c,\mu)$ 得到的）随机样本的，所以具有随机性，我们只能保证学到好模型的概率很大，而这由参数 $\delta$ 来控制。对比以前我们讨论过的学习问题的真实风险的界的时候，实际上就得到了许多问题的可学习性的刻画，那里我们通常是在固定概率 $\delta$ 和训练样本的个数 $n$ 的情况下，得到对应的误差上界 $\epsilon$ 实际上是关于 $\delta$ 和 $n$ 的一个函数。这里我们通常更关心的是给定 $\epsilon$ 和 $\delta$ 的情况下，$n$ 需要达到多少才能实现所要求的精度保证，这通常也称为样本复杂度 (Sample Complexity) 。

这里顺便可以解释一下 PAC (Probably Approximately Correct) 这个名字（不要把 PAC 和 PCA 搞混了），所谓 Approximately Correct 就是指学出的模型的误差比较小（被 $\epsilon$ 限制住），因为实现零误差（absolutely correct) 是非常困难并且通常没有必要的，所以这里考虑的是 Approximately Correct ；其次，由于随机性的存在，我们只能从概率上保证 Approximately Correct 的可能性是很大的（至少 $1-\delta$ 的概率），这就是该模型的名字由来。

上面的两个定义中，第一个定义是仅从统计上来考虑问题，问题是否 Learnable ，如果在这个意义下都不 Learnable 的话，就不太好玩了。在统计意义下 Learnable 之后，第二个扩展的定义再考虑计算量的问题：Learning 是否可在多项式时间内实现，这就更接近计算理论里考虑的问题了。当然，对于实际的问题来说，这是相当重要的一个因素。不过在上面关于 efficiently PAC learnable 的定义中有一些模糊的地方，一个是关于输入空间 $X$ 的维度——如果 $X$ 只是一个抽象空间或者其他奇怪的空间的话，这里的维度应该指什么呢？另外就是 target concept $c$ 的大小是指什么？这些概念通常从直观上是可以理解的，不过这里我们不想陷入过多的关于计算理论方面的讨论，那还将涉及到同一个 concept 以不同的 representation scheme 来表达可能会有不同的“大小”的问题，对这方面感兴趣的同学可以参考 Michael J. Kearns 和 Umesh V. Vazirani 的书《An Introduction to Computational Learning Theory》。这里顺便 8g 一下，Michael Kearns 是 Leslie Valiant 的学生，当然也为 PAC 模型的发展做出了重要贡献咯，而 Leslie Valiant 就是今天的封面人物，提前介绍一下，PAC 模型就是他提出来的，现在在 Harvard ，2010 年图灵奖得主：

For transformative contributions to the theory of computation, including the theory of probably approximately correct (PAC) learning, the complexity of enumeration and of algebraic computation, and the theory of parallel and distributed computing.

下面再回到主题，作为一个例子，我们不妨来简单介绍一下书上的一个经典的例子。这里取 $X\subset\mathbb{R}^2$ 是二维平面上的一个有界子集，要求有界是为了方便在上面定义一个概率测度，不妨就取归一化的 Lebesgue 测度，而 concept class $\mathcal{C}$ 是 $X$ 上的所有矩形的集合，也就是说，对于任意 $c\in\mathcal{C}$ ，它实际上是一个 binary function （矩形形状的子集），对于任意属于该矩形的点 $x$ 有 $c(x)=1$ ，否则 $c(x)=0$ 。现在我们声称 $\mathcal{C}$ 是可学习的，并给出一个具体的学习算法。

下面是一个示意图，黑框表示（未知的）target concept $c$ ，暂且先无视红框，$EX(c,\mu)$ 会根据 $\mu$ 随机地采样到点，如果点在黑框内部，则对应的 label 会是 1 （图中以 + 标识），如果点在黑框外部，对应的 label 会是 0 （图中以 – 标识），现在的目标是要找到 $c$ 的一个 $\epsilon$ 近似：

这里我们采用一种非常简单的算法：直接无视 label 为 0 的数据点，而计算包含了所有 label 为 1 的点的最小的矩形为当前的近似 $\hat{c}$ ，如上图中的红框就是在观察到了图中的这些数据点之后的学习结果。接下来我们来证明这个简单的算法是可以实现 efficient PAC learning 的。

目的要是使得 $\hat{c}$ 是 $c$ 的 $\epsilon$ 近似，也就是说，$\hat{c}\Delta c\leq \epsilon$ 。由于正例（label 为 1 的点）总是在 $c$ 的内部的，因此我们的预测 $\hat{c}$ 也总是会在 $c$ 的内部，于是 $\hat{c}\Delta c=c-\hat{c}$ ，我们可以分为四个部分来考虑问题，首先是上面部分：

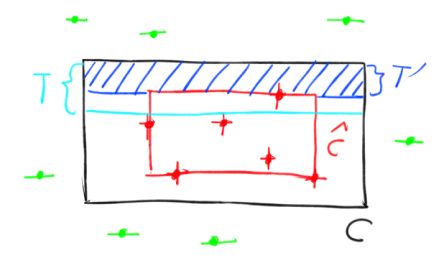
令 $T$ 是从 $c$ 的顶部开始往下的一个测度刚好等于 $\epsilon/4$ 的矩形，并记 $c$ 和 $\hat{c}$ 之差在顶部产生的矩形为 $T’$ ，见上图。当然，我们希望把 $T’$ 限制在 $T$ 以内，这样它的测度讲小于 $\epsilon/4$ ，如果把四个边都限制在 $\epsilon/4$ 之内的话，那么显然 $c-\hat{c}$ 就小于 $\epsilon$ 了（重叠部分不用去管它，因为它并不影响我们的不等式）。

然后我们再回过头来看如何限制 $T’$ ，首先，$\mu(T’)>\epsilon/4$ 当且仅当 $T$ 真包含于 $T’$ ，根据 $\hat{c}$ 的定义，这又当且仅当我们所采样到的训练样本没有落在 $T$ 中，因为，如果有样本 $x$ 落在 $T$ 中，那么由于它又是属于矩形 $c$ 的，所以它的 label 是 1 ，于是，根据定义， $\hat{c}$ 的上边界应该至少在 $x$ 的位置，这与 $T$ 真包含于 $T’$ 是矛盾的。

这样一来，为了限制事件 $\mu(T’)>\epsilon/4$ 的概率，我们可以等价地限制事件“没有样本点落在 $T$ 中”的概率。由于 $T$ 的测度为 $\epsilon/4$ ，所以根据 $\mu$ 采样一个样本点不落在 $T$ 中的概率为 $1-\epsilon/4$ ，如果我们一个采样了 $n$ 个点，那么它们全都不落在 $T$ 中的概率为 $(1-\epsilon/4)^n$ 。

其他三个矩形边上可以用同样的分析。然后，根据概率公式 $P(A\cup B)\leq P(A) + P(b)$ ，我们知道，四个边界上“至少有一个边界有 $\mu(T’)>\epsilon/4$ ”这件事的概率小于等于 $4(1-\epsilon/4)^n$ 。

因此，如果我们有 $4(1-\epsilon/4)^n\leq \delta$ ，则反事件“所有四个边界上都满足 $\mu(T’)\leq\epsilon/4$ ”的概率将大于等于 $1-\delta$ ，而前面的分析知道，那个事件是能推出 $c\Delta\hat{c}\leq\epsilon$ 的，于是，我们达到目的了。

当然，达到目的的前提是 $4(1-\epsilon/4)^n\leq \delta$ ，为了使得形式简单一点，我们这里用一个简单的缩放公式（对 $e^{-x}$ 在 0 处进行泰勒展开就可以得到） $e^{-x}\geq 1-x$ ，因此，为了满足 $4(1-\epsilon/4)^n\leq \delta$ ，我们只需要保证

\[
4e^{-n\epsilon /4}\leq \delta
\]

即可，解出 $n$ 得到：

\[
n\geq \frac{4}{\epsilon}\ln\frac{4}{\delta}
\]

所以，只要我们通过 $EX(c,\mu)$ 得到足够多的数据（至少如上面这个式子这么多），我们就能保证以至少 $1-\delta$ 的概率满足 $c\Delta\hat{c}\leq\epsilon$ ，由于这对任意 $\epsilon$ 和 $\delta$ 都成立，因此我们证明了该 concept space 是 PAC learnable 的。至于计算复杂度，我们的算法几乎不用做任何计算，只要不断地获取数据，直到得到了足够多的数据，然后在简单地遍历一遍数据就可以得到最小的 bounding 矩形，即 $\hat{c}$ 。因此主要的“计算”复杂度在获取数据这个步骤上，又由于我们需要的数据量 $n$ 是 $O(1/\epsilon)$ 以及 $O(1/\delta)$ （实际上还有一个 $\ln$ 函数，因此情况更好一些）的，所以也保证了 efficient PAC learnability 。这里得到的关于样本数目的界，就是这个问题的样本复杂度 (Sample Complexity) 了。

不过我觉得这个例子似乎有一点小问题，主要在于 PAC 模型还要求对任意概率测度 $\mu$ 都是成立的，但是如果是任意奇怪的测度，上面分析中的 $T$ 是否还是一定能取得到呢？不过，如果对 $\mu$ 做一些合理的限制，比如在这里要求对于平面上的 Lebesgue 测度是绝对连续的，应该就没有问题了。这样应该可以把 PAC 模型里的“任意测度”这个条件稍微弱化一下就可以了。反正这里展示的 PAC 模型也是最简单的原型了，在不同的问题中会有各自不同的扩展和推广出现，总之主题思想是那样就可以了。

不过，不管怎么看，这个模型都有点过于简单了，至少和我们最开始做的统计学习的设定相比起来，仅限于 binary classification 这一点就不说了，统计学习中的许多分析也都这样子的。另一个比较明显的限制就是假设 target concept $c$ 没有随机性，似乎各种用 PAC 模型进行分析的时候都喜欢用这种假设，当然简化的模型便于更清楚地分析问题是没错，但是如果因此而使得得到的模型限制过大无法用到具体问题中的话，就显得有些本末倒置了。不过我们这里不妨细看一下这个问题。

一方面，带随机性的模型是包含了无随机性的模型作为一个特例的，那反过来呢？假设我们有 $\mathcal{X}\times\mathcal{Y}$ 上的一个联合概率分布 $\nu$ （这里我们只考虑 binary classification ，也就是 $\mathcal{Y}=\{0,1\}$ 的情况），当然，如果条件分布 $\nu(Y|X=x)$ 不是退化的话，我们是无法用一个非随机的函数 $c:\mathcal{X}\rightarrow\mathcal{Y}$ 来描述这个分布的，但是注意到机器学习的问题并不是要去求这个真实的分布，而是要去求一个风险最小的分类器 $f$ ，而在最开始的关于机器学习问题设定的文章中我们曾经得到一个公式：

\[
R(f)-R(f^*) = \mathbb{E}_X\left[ (2\eta(x)-1)(\chi_{f(x)=0)}-\chi_{f^*(x)=0}) \right] \geq 0
\]

这里 $\eta(x)$ 是回归函数，而 $f^*$ 是根据回归函数定义的 Bayes 分类器。另外，容易验证

\[
\mathbb{E}_X\left[ (2\eta(x)-1)(\chi_{f(x)=0)}-\chi_{f^*(x)=0}) \right] = \mathbb{E}_X\left[ |2\eta(x)-1|\chi_{f(x)\neq f^*(x)} \right]
\]

这里如果把 Bayes 分类器 $f^*$ 看成是 target concept 的话，这个式子其实已经很像普通的无随机性的模型里所定义的误差了，只要使用一个 $\mathcal{X}$ 上的新的概率分布，在每一点按照 $|2\eta(x)-1|$ 重新赋予一下权重即可。因此，对于一个有随机性的问题，从理论上来说，我们通过把它的 Bayes 分类器看成 target concept ，再重新定义一个带权重的 $\mathcal{X}$ 上的分布，从而把原来的问题转化为一个确定性的问题，并由上面的等式知道两个问题所求出来的最优解将会是相等的。所以说，从这种意义下来说，两种模型是可以相互转化的。

这里还可以顺便看一下重新赋予的权重 $|2\eta(x)-1|$ 的“物理”意义：回忆一下回归函数的定义，$\eta(x)=0$ 和 $\eta(x)=1$ 表示 $X=x$ 的情况下 $Y$ 分别确定地（以概率 1）等于 0 和 1 ，此时按照 Bayes 分类器的定义，知道 $f^*$ 的分类结果肯定是对的，而此时权重 $|2\eta(x)-1|=1$ 也达到了最大值；令一个极端情况是 $\eta(x)=0.5$ ，此时 $Y=0$ 和 $Y=1$ 的概率都相等，Bayes 分类器也没办法，它再怎么也有 50% 的概率会搞错，而此时有趣的是权重 $|2\eta(x)-1|=0$ 也达到了最小值 0 ，表示在这一点上即使我们学习出来的分类器和 Bayes 分类器的结果不想等也没关系，因为 Bayes 分类器自己也搞不清楚嘛。所以说，这里的权重实际上是根据 Bayes 分类器的“置信度”来进行了重新赋权重。 🙂

除了随机性之外，我们刚才的 PAC 模型还有一个非常巨大的限制就是要求 target concept $c$ 是属于学习用的 concept space $\mathcal{C}$ 的，这对问题造成了非常大的简化，这种情况通常称为 realizable case ，而更通用的情况是不对 target concept $c$ 做任何限制，通常称为 Agnostic Learning 。这看起来很简单的一个扩展，实际上就一下子把原来很简单的一个问题变得很复杂了（看看它有这么文艺的一个名字就知道不是容易对付的家伙呀）。比如说，刚才的方形学习的例子，如果 target concept 是一个圆形（还不考虑其他更复杂的情形），那那个问题是否还是 PAC learnable 呢？用一个矩形去任意逼近以原型似乎是非常困难的哦~ :p

在本文的最后，稍微提一下令一个扩展，叫做 weak PAC learnable ，这里就不给严格的定义了，如果以后有机会再仔细讲吧，大致意思是，普通的 PAC learnability 要求对任意的 $\epsilon$ 和 $\delta$ 都成立，而 weak PAC learnability 则不要这么苛刻，它限制了 $\epsilon$ 的下限，也就是如果对于大于某个 $\epsilon_0$ 的那些 $\epsilon$ 都能实现的话，就称为 weak learnable 的，比如说，你有一个比较简单的算法，只能保证比“随机猜”算法好那么一点，但是却无法达到更高的精度了，那么用这个算法就可以实现 weak learnable ，这样的算法称为 weak learner，而实现正常的 PAC learnability 的算法称为 strong learner 。Michael Kearns （刚才提到过哦）在 1988 年提了这么一个问题：weak learner 能不能变成 strong learner 呢？Robert Schapire 在 1990 年给了确定的答案，传说 Schapire 有一次到中国，碰到一位得道高僧，便用这个问题去请教这位高僧，高僧抚掌大笑，念叨着“三个臭皮匠，赛过诸葛亮”腾云而去，于是 Schapire 得到了顿悟，发现通过组合 weak learner 的方法可以得到 strong learner ，也就是 boosting 。后来在 1995 年 Yoav Freund 和 Robert Schapire 一起发明的 AdaBoost 算法，成为今天机器学习中应用最广的算法之一。

最后，封面人物，唔，这个似乎已经在前面介绍过了，那么祝大家新年快乐吧！ 🙂