 本文是“支持向量机系列”的第三篇,参见本系列的其他文章。
本文是“支持向量机系列”的第三篇,参见本系列的其他文章。
前面我们介绍了线性情况下的支持向量机,它通过寻找一个线性的超平面来达到对数据进行分类的目的。不过,由于是线性方法,所以对非线性的数据就没有办法处理了。例如图中的两类数据,分别分布为两个圆圈的形状,不论是任何高级的分类器,只要它是线性的,就没法处理,SVM 也不行。因为这样的数据本身就是线性不可分的。
对于这个数据集,我可以悄悄透露一下:我生成它的时候就是用两个半径不同的圆圈加上了少量的噪音得到的,所以,一个理想的分界应该是一个“圆圈”而不是一条线(超平面)。如果用 $X_1$ 和 $X_2$ 来表示这个二维平面的两个坐标的话,我们知道一条二次曲线(圆圈是二次曲线的一种特殊情况)的方程可以写作这样的形式:
\[
a_1X_1 + a_2X_1^2 + a_3 X_2 + a_4 X_2^2 + a_5 X_1X_2 + a_6 = 0
\]
注意上面的形式,如果我们构造另外一个五维的空间,其中五个坐标的值分别为 $Z_1 = X_1$, $Z_2=X_1^2$, $Z_3=X_2$, $Z_4=X_2^2$, $Z_5=X_1X_2$,那么显然,上面的方程在新的坐标系下可以写作:
\[
\sum_{i=1}^5a_iZ_i + a_6 = 0
\]
关于新的坐标 $Z$ ,这正是一个 hyper plane 的方程!也就是说,如果我们做一个映射 $\phi:\mathbb{R}^2\rightarrow\mathbb{R}^5$ ,将 $X$ 按照上面的规则映射为 $Z$ ,那么在新的空间中原来的数据将变成线性可分的,从而使用之前我们推导的线性分类算法就可以进行处理了。这正是 Kernel 方法处理非线性问题的基本思想。
再进一步描述 Kernel 的细节之前,不妨再来看看这个例子映射过后的直观例子。当然,我没有办法把 5 维空间画出来,不过由于我这里生成数据的时候就是用了特殊的情形,具体来说,我这里的超平面实际的方程是这个样子(圆心在 $X_2$ 轴上的一个正圆):
\[
a_1X_1^2 + a_2(X_2-c)^2 + a_3 = 0
\]
因此我只需要把它映射到 $Z_1 = X_1^2$, $Z_2=X_2^2$, $Z_3=X_2$ 这样一个三维空间中即可,下图(这是一个 gif 动画)即是映射之后的结果,将坐标轴经过适当的旋转,就可以很明显地看出,数据是可以通过一个平面来分开的:
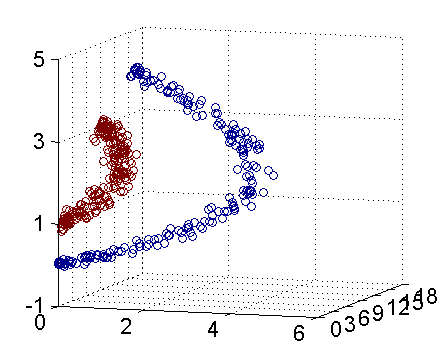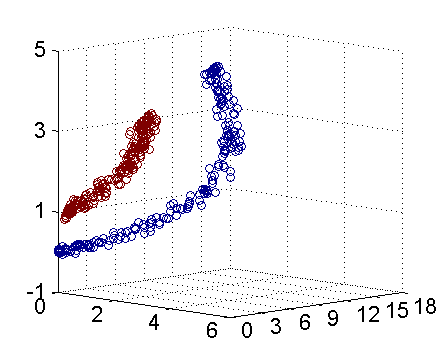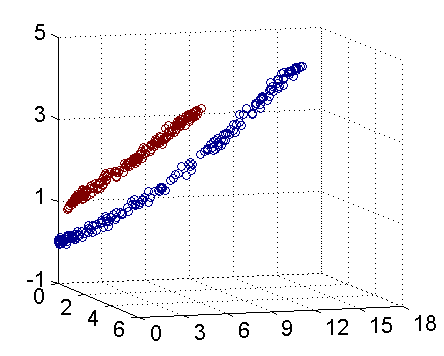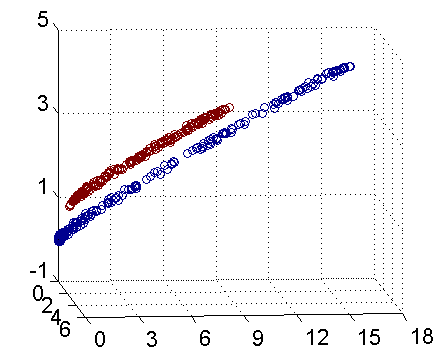
现在让我们再回到 SVM 的情形,假设原始的数据时非线性的,我们通过一个映射 $\phi(\cdot)$ 将其映射到一个高维空间中,数据变得线性可分了,这个时候,我们就可以使用原来的推导来进行计算,只是所有的推导现在是在新的空间,而不是原始空间中进行。当然,推导过程也并不是可以简单地直接类比的,例如,原本我们要求超平面的法向量 $w$ ,但是如果映射之后得到的新空间的维度是无穷维的(确实会出现这样的情况,比如后面会提到的 Gaussian Kernel ),要表示一个无穷维的向量描述起来就比较麻烦。于是我们不妨先忽略过这些细节,直接从最终的结论来分析,回忆一下,我们上一次得到的最终的分类函数是这样的:
\[
f(x) = \sum_{i=1}^n\alpha_i y_i \langle x_i, x\rangle + b
\]
现在则是在映射过后的空间,即:
\[
f(x) = \sum_{i=1}^n\alpha_i y_i \langle \phi(x_i), \phi(x)\rangle + b
\]
而其中的 $\alpha$ 也是通过求解如下 dual 问题而得到的:
\[
\begin{align}
\max_\alpha &\sum_{i=1}^n\alpha_i – \frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j\langle \phi(x_i),\phi(x_j)\rangle \\
s.t., &\alpha_i\geq 0, i=1,\ldots,n \\
&\sum_{i=1}^n\alpha_iy_i = 0
\end{align}
\]
这样一来问题就解决了吗?似乎是的:拿到非线性数据,就找一个映射 $\phi(\cdot)$ ,然后一股脑把原来的数据映射到新空间中,再做线性 SVM 即可。不过若真是这么简单,我这篇文章的标题也就白写了——说了这么多,其实还没到正题呐!其实刚才的方法稍想一下就会发现有问题:在最初的例子里,我们对一个二维空间做映射,选择的新空间是原始空间的所有一阶和二阶的组合,得到了五个维度;如果原始空间是三维,那么我们会得到 19 维的新空间(验算一下?),这个数目是呈爆炸性增长的,这给 $\phi(\cdot)$ 的计算带来了非常大的困难,而且如果遇到无穷维的情况,就根本无从计算了。所以就需要 Kernel 出马了。
不妨还是从最开始的简单例子出发,设两个向量 $x_1 = (\eta_1,\eta_2)^T$ 和 $x_2=(\xi_1,\xi_2)^T$ ,而 $\phi(\cdot)$ 即是到前面说的五维空间的映射,因此映射过后的内积为:
\[
\langle \phi(x_1),\phi(x_2)\rangle = \eta_1\xi_1 + \eta_1^2\xi_1^2 + \eta_2\xi_2 + \eta_2^2\xi_2^2+\eta_1\eta_2\xi_1\xi_2
\]
另外,我们又注意到:
\[
\left(\langle x_1, x_2\rangle + 1\right)^2 = 2\eta_1\xi_1 + \eta_1^2\xi_1^2 + 2\eta_2\xi_2 + \eta_2^2\xi_2^2 + 2\eta_1\eta_2\xi_1\xi_2 + 1
\]
二者有很多相似的地方,实际上,我们只要把某几个维度线性缩放一下,然后再加上一个常数维度,具体来说,上面这个式子的计算结果实际上和映射
\[
\varphi(X_1,X_2)=(\sqrt{2}X_1,X_1^2,\sqrt{2}X_2,X_2^2,\sqrt{2}X_1X_2,1)^T
\]
之后的内积 $\langle \varphi(x_1),\varphi(x_2)\rangle$ 的结果是相等的(自己验算一下)。区别在于什么地方呢?一个是映射到高维空间中,然后再根据内积的公式进行计算;而另一个则直接在原来的低维空间中进行计算,而不需要显式地写出映射后的结果。回忆刚才提到的映射的维度爆炸,在前一种方法已经无法计算的情况下,后一种方法却依旧能从容处理,甚至是无穷维度的情况也没有问题。
我们把这里的计算两个向量在映射过后的空间中的内积的函数叫做核函数 (Kernel Function) ,例如,在刚才的例子中,我们的核函数为:
\[
\kappa(x_1,x_2)=\left(\langle x_1, x_2\rangle + 1\right)^2
\]
核函数能简化映射空间中的内积运算——刚好“碰巧”的是,在我们的 SVM 里需要计算的地方数据向量总是以内积的形式出现的。对比刚才我们写出来的式子,现在我们的分类函数为:
\[
\sum_{i=1}^n\alpha_i y_i \color{red}{\kappa(x_i,x)} + b
\]
其中 $\alpha$ 由如下 dual 问题计算而得:
\[
\begin{align}
\max_\alpha &\sum_{i=1}^n\alpha_i – \frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j \color{red}{\kappa(x_i, x_j)} \\
s.t., &\alpha_i\geq 0, i=1,\ldots,n \\
&\sum_{i=1}^n\alpha_iy_i = 0
\end{align}
\]
这样一来计算的问题就算解决了,避开了直接在高维空间中进行计算,而结果却是等价的,实在是一件非常美妙的事情!当然,因为我们这里的例子非常简单,所以我可以手工构造出对应于 $\varphi(\cdot)$ 的核函数出来,如果对于任意一个映射,想要构造出对应的核函数就很困难了。
最理想的情况下,我们希望知道数据的具体形状和分布,从而得到一个刚好可以将数据映射成线性可分的 $\phi(\cdot)$ ,然后通过这个 $\phi(\cdot)$ 得出对应的 $\kappa(\cdot,\cdot)$ 进行内积计算。然而,第二步通常是非常困难甚至完全没法做的。不过,由于第一步也是几乎无法做到,因为对于任意的数据分析其形状找到合适的映射本身就不是什么容易的事情,所以,人们通常都是“胡乱”选择映射的,所以,根本没有必要精确地找出对应于映射的那个核函数,而只需要“胡乱”选择一个核函数即可——我们知道它对应了某个映射,虽然我们不知道这个映射具体是什么。由于我们的计算只需要核函数即可,所以我们也并不关心也没有必要求出所对应的映射的具体形式。 😀
当然,说是“胡乱”选择,其实是夸张的说法,因为并不是任意的二元函数都可以作为核函数,所以除非某些特殊的应用中可能会构造一些特殊的核(例如用于文本分析的文本核,注意其实使用了 Kernel 进行计算之后,其实完全可以去掉原始空间是一个向量空间的假设了,只要核函数支持,原始数据可以是任意的“对象”——比如文本字符串),通常人们会从一些常用的核函数中选择(根据问题和数据的不同,选择不同的参数,实际上就是得到了不同的核函数),例如:
- 多项式核 $\kappa(x_1,x_2) = \left(\langle x_1,x_2\rangle + R\right)^d$ ,显然刚才我们举的例子是这里多项式核的一个特例($R=1,d=2$)。虽然比较麻烦,而且没有必要,不过这个核所对应的映射实际上是可以写出来的,该空间的维度是 $\binom{m+d}{d}$ ,其中 $m$ 是原始空间的维度。
- 高斯核 $\kappa(x_1,x_2) = \exp\left(-\frac{\|x_1-x_2\|^2}{2\sigma^2}\right)$ ,这个核就是最开始提到过的会将原始空间映射为无穷维空间的那个家伙。不过,如果 $\sigma$ 选得很大的话,高次特征上的权重实际上衰减得非常快,所以实际上(数值上近似一下)相当于一个低维的子空间;反过来,如果 $\sigma$ 选得很小,则可以将任意的数据映射为线性可分——当然,这并不一定是好事,因为随之而来的可能是非常严重的过拟合问题。不过,总的来说,通过调控参数 $\sigma$ ,高斯核实际上具有相当高的灵活性,也是使用最广泛的核函数之一。
- 线性核 $\kappa(x_1,x_2) = \langle x_1,x_2\rangle$ ,这实际上就是原始空间中的内积。这个核存在的主要目的是使得“映射后空间中的问题”和“映射前空间中的问题”两者在形式上统一起来了。
最后,总结一下:对于非线性的情况,SVM 的处理方法是选择一个核函数 $\kappa(\cdot,\cdot)$ ,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。由于核函数的优良品质,这样的非线性扩展在计算量上并没有比原来复杂多少,这一点是非常难得的。当然,这要归功于核方法——除了 SVM 之外,任何将计算表示为数据点的内积的方法,都可以使用核方法进行非线性扩展。
此外,略微提一下,也有不少工作试图自动构造专门针对特定数据的分布结构的核函数,感兴趣的同学可以参考,比如 NIPS 2003 的 Cluster Kernels for Semi-Supervised Learning 和 ICML 2005 的 Beyond the point cloud: from transductive to semi-supervised learning 等。

请问你用什么工具画旋转图的?
这个是用 Matlab 画出一张张图片然后用 Imagemagick 拼贴成的 gif 动画。
图很好看 😀
请问kid大人的blog接受投稿吗?
文西你想写什么?要是写得有趣,可以在我这里发布。
哈哈,上个月看到kid和caideng发在sigkdd2010上的论文。然后就找到了这个blog。昨天周昆报告会的时候还看见你了。做最中间吧。仰慕啊!
呵呵,你好。呃,尴尬啊,我不知道昨天周老师有报告会啊,所以我肯定没在,你认错人了 :p
我昨天上caideng人工智能时就知道不是你了,是TA(Lin Yue)。⊙﹏⊙b汗。我没有见过你都以为是你!囧
呵呵~
[…] 支持向量机:Kernel —— 介绍核方法,并由此将支持向量机推广到非线性的情况。 […]
“其实刚才的方法稍想一下就会发现有问题:在最初的例子里,我们对一个二维空间做映射,选择的新空间是原始空间的所有一阶和二阶的组合,得到了五个维度;如果原始空间是三维,那么我们会得到 19 维的新空间(验算一下?)”
你忘了说明三维情况下是对所有”三阶”的组合,得到的才是19维空间。
对核函数多了一些了解!
难读的是你文中用来说明”核函数是表达向量在映射后空间中内积的函数”的例子,先有大X来表示维度,后有小x来表示向量了;最后大X和小x的表达凑到了一起:
Fi(x) = Fi(X1, X2) = …
这是不是读得有点儿痛苦。可能澄清下小x和大X之间的区别会比较好。
是不是可以这样理解,小写 $x$ 表示向量,大写 $X_i$ 表示第 $i$ 个坐标,或者说坐标函数,比如如果向量 $x=(2,4,6)$ ,那么 $X_2(x) = 4$ 。如何?不想用小写字母加下标是因为会和不同数据点的下标混淆,用上标写也会很麻烦,和指数混在一起了……
恩,这样子显式说明会比较不容易误解吧。
“具体来说,下面这个式子的计算结果实际上和映射…
…(自己验算一下)。”
这里的“下面的式子”就是指上面核函数的式子.
还有这里突然出现的X1,X2的确很不和谐啊,用η1,η2不是更好?
我觉得这里写成 phi((X1, X2)) , 多加一个括号就不会有误会了
“这个核存在的主要目的是使得“映射后空间中的问题”和“映射前空间中的问题”两者在形式上统一起来了”
不是很明白这句话的意思,这个线性核表达的是向量在原空间中的内积。所以是自己映射到自己,也就是没有映射喽?
你说的“映射后空间中的问题”和“映射前空间中的问题”相统一是具体指什么呀?(什么问题、统一了什么)
Thanks!
就是说,你写公式,或者是写代码的时候,可以只写一个,然后代入不同的核,就能分别得到线性和非线性的情况,于是两者就统一起来了,不用分别写一个线性的,再写一个非线性的。
喔,原来如此。
第三段Z_2 = X_1^2 写成 X_2 = X_1^2了
blog写的很赞啊 要是有些什么数据的优化方法什么的就更好啦:-)
啊!多谢指出!已经修正~
真不错啊
[…] 支持向量机: Kernel /?p=685 […]
你好,能不能告诉我你的第一幅图 two circle, 如何用matlab生成这样的数据?谢谢啦
你好,就是在两个不同半径的圆圈上分别采集一些点然后加上一些高斯噪声啦。
还是不太会。。能看一下你的生成数据的代码吗?呵呵
额……这个当时在 matlab 里输入了命令生成了就没了,没有保存代码啊。你去看一下 matlab 里生成随机数啊之类的相关函数吧。
我写了一个,呵呵,语法比较朴素。。
alpha=0:pi/50:2*pi;
R=10;
x=R*cos(alpha);
y=R*sin(alpha);
R1=5;
x1=R1*cos(alpha);
y1=R1*sin(alpha);
list1 = randperm(length(alpha));
x3 = x(list1(1:70));
y3 = y(list1(1:70));
list2 = randperm(length(alpha));
x4 = x1(list2(1:70));
y4 = y1(list2(1:70));
y3 = y3 + rand(1,70);
y5 = y3 – rand(1,70);
y4 = y4 + rand(1,70);
y6 = y4 – rand(1,70);
plot(x3,y3,’bo’)
hold on
plot(x4,y4,’ro’)
plot(x3,y5,’bo’)
plot(x4,y6,’ro’)
哈哈,非常感谢,Thanks!
那个gif的图简直美死了
我觉得我在不停的窃取你的东西呢,我好内疚啊,我下周二毕业答辩,在做presentation 的讲稿,用了你好多图,我一定在毕业论文中感谢你哈,其会将你博客正确引用在referance中,实在不行的话,等我答辩完,给你寄一本我的论文当做感激好了,这样抄的我也心安理得些
哈哈,谢谢谢谢!
不过我写的就是科普贴和总结贴啦,reference 最好还是找专门的论文啦! 🙂
祝答辩顺利!
[…] 支持向量机:Kernel —— 介绍核方法,并由此将支持向量机推广到非线性的情况。 […]
A good intro!
下面这个式子的计算结果
应该是 “上面” 才对吧.
嗯,谢谢!似乎确实是写错了!
不晓得R是不是可以直接作出这个gif动画图像。
关键是R不晓得有没有支持 SVM的包
那个映射,画图的maple程序是:
with(plots);
p1 := plot([sin(theta), cos(theta), theta = 0 .. 2*Pi], color = blue);
p2 := plot([2*sin(theta), 2*cos(theta), theta = 0 .. 2*Pi]);
plots[display]({p1, p2});
p3 := plot3d([sin(theta)^2, cos(theta)^2, cos(theta)], theta = 0 .. Pi, z = -1 .. 1, color = blue);
p4 := plot3d([(2*sin(theta))^2, (2*cos(theta))^2, 2*cos(theta)], theta = 0 .. Pi, z = -1 .. 1);
plots[display]({p3, p4});
大家在maple中可以用鼠标拖动三维图看看,很形象的一个降维的例子。帮助大家理解为什么有时需要降维,有时又需要升维。
打错了,应该是升维的例子。我猜降维通俗的理解其实就是投影吧?降维以后好多信息都隐藏掉了,我们看不到。所以三维的人很难想象一个四维空间里的东西是什么样的。
Just want to thank you for the nice post. I was always confused about the Kernel trick, but got a lot more clear reading your articles.
你好世界!
[…] 我们可以让空间从原本的线性空间变成一个更高维的空间,在这个高维的线性空间下,再用一个超平面进行划分。这儿举个例子,来理解一下如何利用空间的维度变得更高来帮助我们分类的(例子以及图片来自pluskid的kernel函数部分): […]
&(x1,x2) = (根号下2 x1, x1的平方… 这一步是怎么算的,z1不是只对应一个坐标吗,可是这个括号里友两个坐标
看懂了 原来&(x1,x2) = &( k(x1,x2)) = &((+1)) 对吧, SVM有很多数学知识要懂
我刚才看了下bioshop 295页上 有句话是the Gram matrix K, whose elements are given by K(xn, xm) should be positive semidefinite for all possible choices of the set {xn}. => xMx >0; 这里x是坐标, M是matrix
您好!请问分类函数f(x)中的b是怎么确定的?
你好,那个可以算出来的,具体可以参见 Andrew Ng 的课程 slides: http://cs229.stanford.edu/notes/cs229-notes3.pdf
您好,感谢您的分享,想请教文中有关高斯核参数σ 的选取带来的影响,”σ选得很大的话,高次特征上的权重实际上衰减得非常快,所以实际上(数值上近似一下)相当于一个低维的子空间;反过来,如果 σ 选得很小,则可以将任意的数据映射为线性可分”该怎么理解呢,能进一步解释一下吗?比如这个”高次特征“是指?特征上的权重又是指什么呢?为什么”σ 选得很小,则可以将任意的数据映射为线性可分“呢?抱歉之前对核函数学习的比较少,或者有关这个结论的理解和证明可以参看什么资料吗?非常感谢!
你好,抱歉我有点不太记得当时说“高次特征”是指什么了,可能是为了类比多项式核这种有限维的情况。当然直观上理解也并不是很困难,关于线性可分,实际上可以把线性分类器的方程写出来,可分就是指那个方程有解,它会等价于 kernel matrix 是非奇异的。然后在来看 σ 的选取:σ 很小的时候,核矩阵会近视等于单位矩阵,这个从 Gaussian kernel 的表达式也可以看出来,这个时候核矩阵是非奇异的; σ 很大的时候呢,不妨想像得夸张一点,注意 Gaussian Kernel 的表达式,不管你两点间距离多大,我总是可以选到相当大的 σ ,使得 exp 指数上那个数接近于零——数值舍入一下就等于零的话,那么核函数的值就等于一了,这样一来会得到一个所有元素(近视)全是一的矩阵,它明显是奇异的,也就不可分了。
关于 kernel 的更多的资料的话,可以参考《Learning with Kernels》这本书。
感谢您的回复,虽然不太明白为什么“线性分类器的方程有解等价于 kernel matrix 是非奇异的”(这一结论在关于核函数的学习研究中是已经证明了的吗,比如您推荐的《Learning with Kernels》这本书里就有答案吗,或者能否指给一个参考文献呢),但是基于这个结论来理解 σ 取值带来的影响就容易多了,谢谢您。这样一来的话,实际应用中核函数参数的选取是否都能以此结论为指导来学习,而不用再在某一取值范围内搜索最优值了呢?感觉好多算法在实际应用中,参数才是决定最终性能的关键,在有充足训练样本的情况下还可以调节,没有的话就很难保证算法性能了。因为学习的很有限,看的算法对参数的鲁棒性提及都不多,关于参数以及超参数的学习方面有没有一些推荐呢?非常感谢!
你好,你可以尝试写一下 Kernel Least Square 的解的解析形式,这个形式要有意义,就要求 Kernel matrix 是非奇异的。这只是一个比较 general 的准则,并没有办法帮助我们选择具体的参数数值。而且许多理论上的关于参数的结论都由于 bound 过于松散的原因,在实际中效果也并不好,实际中一般仍然是用 cross-validation 之类的方法来搜索最优参数的方式比较多一点。
非常好的文章,简单通俗易懂
博主写的太好了,通俗易懂,支持下。如果我想要引用您的那个旋转的图,可以么,那我reference该怎么写呢
ESL的书看不懂 跑来看你的blog 很受益
谢谢前辈写文章。
这学期看Mehryar Mohri的Foundations of Machine Learning,简直看得一头雾水,在网上查资料,搜到博主的文章,看完之后恍然大悟,确实深入浅出!推荐!!
非常好,着重点恰到好处
你好,我是一名学生,研究直方图交叉核函数好长时间。但是一直弄不懂它为什么能用于图像的分类。请问您能不能帮忙解释下直方图交叉核函数也叫做min kernel ,为什么能用于图像的分类识别,就是它相对于其他核函数来说在图像分类方面有什么优势?
高斯核中,σ为函数的宽度参数, 控制了函数的径向作用范围,我实在是不是很理解这句话。跪求楼主解答。。而且。还有。为什么随着西格玛的增大。支持向量的个数会减少(我自己在R上模拟出来的结果)?谢谢~
你好,sigma 的大小控制核函数随着数据点之间的距离而衰减的速度,例如 sigma 很小的话,距离较远的点的核函数值就已经很接近 0,差不多可以忽略不计了。sigma 越小实际上过拟合也越严重,反过来 sigma 越大的话,我想应该可以简单地理解为 training data 上不能被分隔在 margin 之外的点越多,所以支持向量就越多了。
如果原始空间是三维,那么我们会得到 19 维的新空间(验算一下?)
你好,问一下,这个有木有算法可以计算的?
比如说,n维变量升维会有多少种情况?
有一个小疑问:
虽然比较麻烦,而且没有必要,不过这个核所对应的映射实际上是可以写出来的,该空间的维度是 (m+d,d) ,其中 m 是原始空间的维度
这里的 该空间的维度 应该是(m+d ,d) -1 ?
从上文的二维映射到五维空间的说法中验证得出
还有常数维度呢?
[…] 我们可以让空间从原本的线性空间变成一个更高维的空间,在这个高维的线性空间下,再用一个超平面进行划分。这儿举个例子,来理解一下如何利用空间的维度变得更高来帮助我们分类的(例子以及图片来自pluskid的kernel函数部分): […]
谢谢博主,讲的很清楚!
建议向量和分量还是要区分一下统一写,例如这里的空间映射函数phi(x):R^2->R^5,
感觉写为: phi(x)=(x1,x1^2,×2,x2^2,x1x2)更好懂些。
关于kernel函数,也推荐另外一篇写得很清晰的文章:
谢谢博主大神的详细讲述!
想请教一个问题:
为什么高斯核刚好也是向量映射到高维的内积呢?
因为根据 Mercer’s Theorem,一个 symmetric positive definite 的核函数会对应一个 RKHS。
博主,对于kernel SVM,如果训练样本数太多的话,是不是会因为核矩阵太大而产生一些问题?
是的。
在没有使用kernel的SVM中,其目标函数中包含了样本内积(x_i*x_j);
使用kernel之后,以上的部分可以用映射以后的新特征空间内积替代(即核函数);
请问为什么能这么做?
这样做不是改变了SVM的目标函数吗?对优化应该产生影响的啊?!
我不知道问题你有没有明白。。。呵呵,请见谅~
另,感谢你的文章~
因为数据点线性不可分,所以要对数据点x升维度,升了维度之后使用$\phi(x)$本身就不是原优化问题了。
然后观察新优化问题,我们发现$\phi(x)$从来都不单独出现而永远出现在一个内积中,所以干脆我们就用核函数K(x, x’)来计算$\phi(x) \phi(x’)$,在能找到这么一个核函数的前提下。
顺便提个建议啊,怎么让评论也能使用mathjax啊~
可以理解成,核函数起的作用是,把低维眏射到高维吗?
向大牛学习~
谢谢博主的文章。有一个疑问,对于文中的线性不可分的数据集,最直观的分界肯定是两个圆中间的圆形分界线。如果通过核方法映射到高维空间之后,数据集变成线性可分了,此时SVM对应的分离超平面与原数据集中的圆形分界线是也是对应的吗?就是说在特征空间里的最优分隔超平面对应到原始空间内还是最优分隔面吗?
又看了一眼动图,貌似不是。
原始数据集中的圆形分隔面对应到特征空间里,应该还是两个数据集中间的那条曲线。这样看来SVM选择的分离超平面似乎是一个比较差劲的分隔面啊,因为数据稍微有些扰动,这个超平面就会预测错误。所以SVM强行用线性分类器去分隔线性不可分的数据集,会不会导致得到的分类器鲁棒性较低呢?
非常感谢,还不会提问题,先窥探一下奥秘