Generate Recursive Images

在上一篇 blog 中我提到了递归图片，还给了一个有趣的例子，这次还说递归图片，再给另一个例子：

不过这次的例子是我自己生成的，而篇 blog 就是要讲如何来生成这样一张递归图片。其实方法很简单，类推一下，多花一些功夫的话，之前给的那个“二次递归”的例子也是可以“轻松”做出来的。 🙂

秘密就在于不动点迭代。我在上一篇 blog 中已经说过了，这个递归的东西要找的其实是一个“不动点”。对于一个函数 $f$ 来说，一个不动点 $x$ 就是满足 $f(x)=x$ 的值。而不动点的求法就是一个迭代，简单来说，就是随便找一个初始值 $x_0$ ，带进函数里得到 $x_1=f(x_0)$ ，然后再带回去得到 $x_2=f(x_1)$ ，如此迭代，如果数列 $\{x_i\}$ 收敛的话，极限 $x^*=\lim_{i\rightarrow \infty}x_i$ 将会是 $f$ 的一个不动点。

不过，因为我见过的用不动点迭代来求解的情况 $f$ 都是比较简单的可以写出解析式的函数，由于思维定式，我觉得图片的情况应该会很复杂没有办法这样来解。后来由 van 大神的提点，让我混乱的思维渐渐清晰起来，其实只要这个函数可以求值就好了，并不需要太多的其他条件，如果迭代收敛的话，就可以得到想要的递归图片了！

具体来说，现在我们有一张大图，里面有一个小框，这个小框里将包含这个大图本身的一个缩小版本，当然，缩小版本里还有更小的版本，如此递归。我们令 $x$ 为所求的递归图的话，那么令 $x=f(x)$ 为不动点迭代的函数，这里的 $f$ 其实代表了这样的操作：把 $x$ 缩小，然后再贴到一个背景图上去（这个背景图就是最开始的那张大图里除去那个小框的部分。当然，这个函数如果要写出解析式也许是很复杂，但是给定一张图片作为输入，要求出经过这些运算过后的结果是很简单的，那这样是不是就可以求出前面的递归图片了呢？

我写了简单的 Matlab 代码来验证，随便找了一张场景类似的图来做试验，代码里面硬编码了许多数字，就不要说我代码丑了啊！ :p

ratio = 0.45;
pi = 759; pj = 1496;
w = 1914; h = 1254;
Nit = 100;
threshold = 10;
 
img = imread('input.jpg');
x = img;
 
for iit = 1:Nit
   xsmall = imresize(x, ratio);
   xnew = img;
   xnew(pi:pi+h-1, pj:pj+w-1,:) = xsmall(1:h,1:w,:);
 
   diff = x-xnew;
   diff = sum(sum(sum(diff.*diff)));
   if diff < threshold
       break;
   end
 
   x = xnew;
   imwrite(x, sprintf('iter-%02d.jpg', iit), 'jpg');
end

结果异常好，这是一张 4272×2848 的图片，在 12 步之内就收敛了，结果就是上面的图。下面再看一张迭代第二步的图：

可是，仔细一点看，有没有发现问题？作弊呀！这明明就是把图片不断缩小贴到那个地方这么一个简单的步骤嘛，什么不动点呢？所谓“收敛”其实就是图片缩小到看不清楚了为止吧！嗯，确实没错，过程就是这样的，但是并不是在作弊，因为这个就是不动点迭代呀，我想数学最美妙的地方应该就在于那些可以很直观地表现为一种简单明了的过程的一些东西了吧。

用同样的方法，加上一些复杂一些的变换，诸如旋转呀，甚至三维扭曲呀之类的，可以做出更 cool 的图来，而之前那篇 blog 里的那张双重递归的图，应该也是可以用双重嵌套迭代的方法求出来了。哎呀，好像原本很有意思的东西被这样一摆明了，倒是觉得有些无聊了。 -.-

不过，如果你感兴趣的话，关于不动点迭代，我还可以多说两句。通常讲到不动点迭代求解通常都会举的一个例子是迭代法求平方根，例如，要求 $\sqrt{a}$ 怎么求？写出一个迭代方程 $x=f(x)=0.5(a/x + x)$ （如果你已经发现了，没错，这就是用牛顿法来求方程 $a-x^2=0$ 的根得到的式子），很显然，如果 $x=\sqrt{a}$ ，那么 $x=f(x)$ 是成立的，所以说 $x=\sqrt{a}$ 是它的一个不动点。那么反过来用不动点迭代法求 $\sqrt{a}$ 需要满足什么条件呢？首先是这样产生出来的数列是收敛的，第二是该式子的不动点是唯一的：因为如果不唯一的话，那么虽然 $\sqrt{a}$ 是它的不动点，但是我们求出来的不动点可能是另一个值，并不等于 $\sqrt{a}$ 。

首先，第一个条件是可以证明的，由迭代公式 $x_{n+1}=0.5(a/x_n + x_n)$ 产生的数列。我们有：

当 $x_n>0$ 时，上式右边非负，且

因此 $\{x_n-\sqrt{a}\}$ 是非负递减的数列，故可证收敛性。同样对于 $x_n < 0$ 的时候是对称的，类似可以证明。显然 $x_n$ 的符号依赖于初值 $x_0$ 的选取，而在迭代过程中是不会改变符号的。由 $\{x_n-\sqrt{a}\}$ 的收敛性可以得到 $\{x_n\}$ 的收敛性。 接下来，关于第二个条件，我们可以直接举出一个反例 $x=-\sqrt{a}$ 也是一个不动点，因此不动点是不唯一的。所以，在这里不动点迭代并不能保证一定会求得我们想要的 $\sqrt{a}$ 这个不动点，而这就和初始值的选取有关系——这也是很多迭代方法的一个通常的毛病。 其实对于这个问题，把图画出来就很明了了，蓝线是 $f(x)$ 的图像，而不动点即该图像与 $g(x)=x$ 这条直线的交点，刚好有两个，对应的是 $\pm\sqrt{a}$：

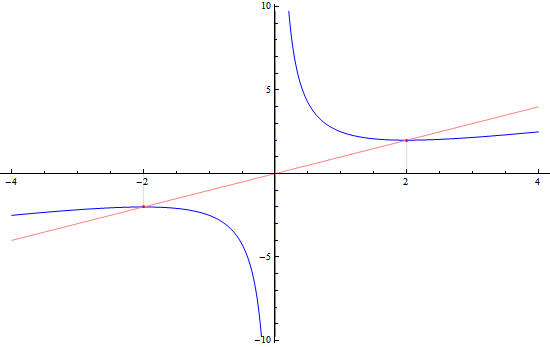
注意上图横纵坐标比例不一样，否则直线应该是 45 度角的。迭代的过程其实就是在 x 轴上取一个点，找出曲线上对应点的纵坐标，作过 y 轴上该纵坐标点出的斜率为 -1 的一条直线，该直线于 x 轴的交点就是新的 x 。这个值会逐渐接近不动点 $x^*$ 。而从图上也可以看出，这里一共就是两个不动点，得到哪个结果刚好取决于初值的正负性。

那么对于其他情况呢？特别是对于我们递归图像的情况呢？这个迭代过程是否收敛呢？要证明这个收敛性似乎就变得非常复杂了。不过，如果从工程师的心态来看的话，那就先试一试好了，如果结果好，那就皆大欢喜了，管他收敛不收敛！ 😀 实际上，这个迭代生成递归图片的方法，从实验来看的话，似乎还是相当好的，就算是初始值取完全随机生成的像素点，也能很快收敛（嗯嗯，那是当然的啦，本身就是一个很简单的复制、缩小、粘贴过程嘛 :p ）。