漫谈 Clustering (番外篇): Dimensionality Reduction

本文是“漫谈 Clustering 系列”中的第 7 篇，参见本系列的其他文章。

由于总是有各种各样的杂事，这个系列的文章竟然一下子拖了好几个月，（实际上其他的日志我也写得比较少），现在决定还是先把这篇降维的日志写完。我甚至都以及忘记了在这个系列中之前有没有讲过“特征”（feature）的概念了，这里不妨再稍微提一下。机器学习应用到各个领域里，会遇到许多不同类型的数据要处理：图像、文本、音频视频以及物理、生物、化学等实验还有其他工业、商业以及军事上得到的各种数据，如果要为每一种类型的数据都设计独立的算法，那显然是非常不现实的事，因此，机器学习算法通常会采用一些标准的数据格式，最常见的一种格式就是每一个数据对应欧几里德空间里的一个向量。

如果原始的数据格式不兼容，那么就需要首先进行转换，这个过程通常叫做“特征提取”（Feature Extraction），而得到的标准数据格式通常叫做 Feature 。例如，一个最简单的将一个文本 Document 转化为向量的方法如下：

1. 选定特征空间，这里采用三维欧氏空间，三个维度（依次）分别由 to 、be 和 the 表示。
2. 假设待提取的文档是“To be, or not to be: that is the question:”，首先对其进行一些预处理，例如去掉单词的时态后缀、滤掉标点符号等，得到“to be or not to be that be the question”。
3. 统计三个维度所对应的单词出现的频率：to 2 次，be 3 次，the 1 次。
4. 该文档对应的向量即 [2, 3, 1] 。

当然，在实际中我们几乎不会这样人工设定空间的各个维度所对应的单词，而通常是从一个数据集中统计出所有出现的词，再将其中的一些挑选出来作为维度。怎样挑选呢？最简单的办法是根本不做任何挑选，或者简单地只是把出现频率太低的单词（维度）去掉。

不过，事实上我们通常会做更复杂一些的处理，例如，如果你是在做 sentiment analysis ，那么你通常会更加关注语气很重的词，比如 “bad”、“terrible”、“awesome” 等的重要性就比普通的词要大，此时你可以为每一个维度设一个权重，例如，给 “bad” 设置权重 2 ，那么出现 3 次的话，向量在该维度对应的值就为 2*3 = 6 。当然这样手工指定权重只在小范围内可行，如果要为数百万个维度指定权重，那显然是不可能的，另一个稍微自动一点的办法是 tf-idf 。

tf 就是 Term Frequency ，就和刚才说的单词出现的次数差不多，而 idf 则是 Inverse Document Frequency ，通常使用如下公式进行计算：

这相当于自动计算出来的每个单词的权重，其想法很简单：如果在许多文档中都出现的词（例如虚词、语气词等），它所包含的信息量通常会比较小，所以用以上的公式计算出来的权重也会相对较小；另一方面，如果单词并不是在很多文档中都出现的话，很有可能就是出现的那些文档的重要特征，因此权重会相对大一些。

前面说了一堆，其实主要是想要对 feature 做一些“预”处理，让它更“好”一些，手工设置维度的权重固然是很人力，其实 tf-idf 也是在假定了原始 feature 是 document 、term 这样的形式（或者类似的模型）的情况下才适用的（例如，在门禁之类的系统里，feature 可能有声音、人脸图像以及指纹等数据，就不能这样来处理），因此也并不能说是一种通用的方法。

然而，既然机器学习的算法可以在不考虑原始数据的来源和意义的情况下工作，那么 feature 的处理应该也可以。事实也是如此，包括 feature selection 和 dimensionality reduction 两个 topic 都有许多很经典的算法。前者通常是选出重要的 feature 的维度（并抛弃不重要的维度），而后者则是更广泛意义上的把一个高维的向量映射为一个低维向量，亦即“降维”，得到的结果 feature 的值已经不一定是原始的值，也可以把 feature selection 看作是 dimensionality reduction 的一种特殊情况。举一个例子，tf-idf 实际上不算 feature selection ，因为它（通常）并没有丢弃低权值的维度，并且处理过后的特征的每个维度都被乘上了一个权值，不再是原来的值了；但是它却可以被看作一种降维，虽然严格意义上来说维度并没有“降低”。简单来说降维可以看作一个函数，其输入是一个 D 维的向量，输出是一个 M 维的向量。

按照机器学习的方法的一贯作风，我们需要定义目标函数并进行最优化。不同的目标也就导致了不同的降维算法，这也正是今天要讲的话题。

然而，我们的目的究竟是什么呢？一个比较直接的问题是原始的数据量维度太高，我们无法处理，因此需要降维，此时我们通常希望在最大限度地降低数据的维度的前提下能够同时保证保留目标的重要的信息，就好比在做有损的数据压缩时希望压缩比尽量大但是质量损失不要太多。于是问题又转化为如何衡量对信息的保留程度了。

一个最直接的办法就是衡量 reconstruction error ，即

其中 $\tilde{\mathbf{x}}_i$ 是 $\mathbf{x}_i$ 所对应的低维表示再重新构造出来的高维形式，就相当于是压缩之后解压出来的结果，不过虽然有许多压缩方法都是无损的，就是说这个差值会等于零，但是大部分降维的结果都是有损的。不过我们仍然希望把上面的 reconstruction error 最小化。

另外一种方式是简单地使用 variance 来衡量所包含信息量，例如，我们要把一些 D 维的向量降为 1 维，那么我们希望这一维的 variance 达到最大化，亦即：

其中 $f$ 是降维函数。推而广之，如果是降为 2 维，那么我希望第 2 维去关注第 1 维之外的 variance ，所以要求它在与第一维垂直的情况下也达到 variance 最大化。以此类推。

然而，当我们把降维函数 $f$ 限定维线性的时候，两种途径会得到同样的结果，就是被广泛使用的 Principal Components Analysis(PCA) 。PCA 的降维函数是线性的，可以用一个 $D\times M$ 维的矩阵 $W$ 来表示，因此，一个 D 维的向量 $\mathbf{x}$ 经过线性变换 $W^T\mathbf{x}$ 之后得到一个 M 维向量，就是降维的结果。把原始数据按行排列为一个 $N\times D$ 维的矩阵 $X$ ，则 $XW$ 就是降维后的 $N\times M$ 维的数据矩阵，目标是使其 covariance 矩阵最大。在数据被规则化（即减去其平均值）过的情况下，协方差矩阵 （covariance） $S = \frac{1}{N}W^TX^TXW$ ，当然矩阵不是一个数，不能直接最大化，如果我们采用矩阵的 Trace （亦即其对角线上元素的和）来衡量其大小的话，要对 $S$ 求最大化，只需要求出 $X^TX$ 的特征值和特征向量，将 M 个最大的特征值所对应的特征向量按列排列起来组成线性变换矩阵 $W$ 即可。这也就是 PCA 的求解过程，得到的降维矩阵 $W$ 可以直接用到新的数据上。如果熟悉 Latent Semantic Analysis (LSA) 的话，大概已经看出 PCA 和 Singular Value Decomposition (SVD) 以及 LSA 之间的关系了。以下这张图（引自《The Elements of Statistical Learning》）可以直观地看出来 PCA 做了什么，对于一些原始为二维的数据，PCA 首先找到了 variance 最大的那一个方向：

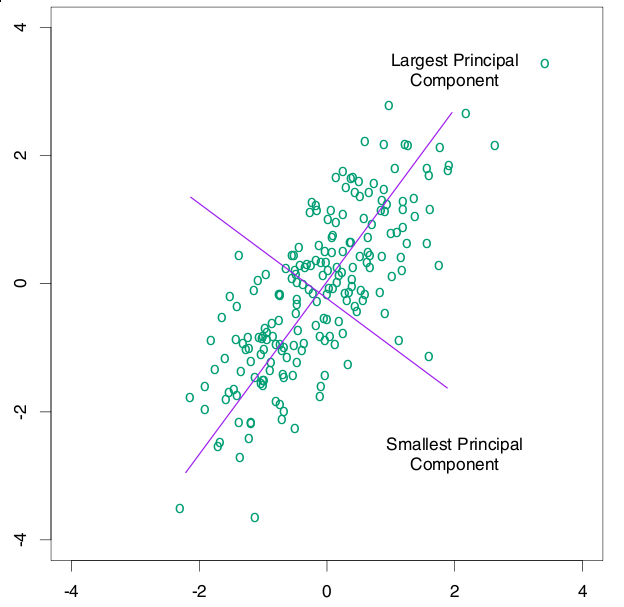
PCA 作为一种经典的降维方法，被广泛地应用于机器学习、计算机视觉以及信息检索等各个领域，其地位类似于聚类中的 K-means ，在现在关于降维等算法的研究中也经常被作为 baseline 出现。然而，PCA 也有一些比较明显的缺点：一个就是 PCA 降维是线性变换，虽然线性变换计算方便，并且可以很容易地推广到新的数据上，然而有些时候线性变换也许并不合适，为此有许多扩展被提出来，其中一个就是 Kernel PCA ，用 Kernel Trick 来将 PCA 推广到非线性的情况。另外，PCA 实际上可以看作是一个具有 Gaussian 先验和条件概率分布的 latent variable 模型，它假定数据的 mean 和 variance 是重要的特征，并依靠 covariance 最大化来作为优化目标，而事实上这有时候对于解决问题帮助并不大。

一个典型的问题就是做聚类或分类，回想我们之前谈过的 Spectral Clustering ，就是使用 Laplacian eigenmap 降维之后再做 K-means 聚类，如果问题定下来了要对数据进行区分的话，“目的”就变得明朗了一些，也就是为了能够区分不同类别的数据，再考虑直观的情况，我们希望如果通过降维把高维数据变换到一个二维平面上的话，可以很容易“看”出来不同类别的数据被映射到了不同的地方。虽然 PCA 极力降低 reconstruction error ，试图得到可以代表原始数据的 components ，但是却无法保证这些 components 是有助于区分不同类别的。如果我们有训练数据的类别标签，则可以用 Fisher Linear Discriminant Analysis 来处理这个问题。

同 PCA 一样，Fisher Linear Discriminant Analysis 也是一个线性映射模型，只不过它的目标函数并不是 Variance 最大化，而是有针对性地使投影之后属于同一个类别的数据之间的 variance 最小化，并且同时属于不同类别的数据之间的 variance 最大化。具体的形式和推导可以参见《Pattern Classification》这本书的第三章 Component Analysis and Discriminants 。

当然，很多时候（比如做聚类）我们并不知道原始数据是属于哪个类别的，此时 Linear Discriminant Analysis 就没有办法了。不过，如果我们假设原始的数据形式就是可区分的的话，则可以通过保持这种可区分度的方式来做降维，MDS 是 PCA 之外的另一种经典的降维方法，它降维的限制就是要保持数据之间的相对距离。实际上 MDS 甚至不要求原始数据是处在一个何种空间中的，只要给出他们之间的相对“距离”，它就可以将其映射到一个低维欧氏空间中，通常是三维或者二维，用于做 visualization 。

不过我在这里并不打算细讲 MDS ，而是想说一下在 Spectral Clustering 中用到的降维方法 Laplacian Eigenmap 。同 MDS 类似，LE 也只需要有原始数据的相似度矩阵，不过这里通常要求这个相似度矩阵 $S$ 具有局部性质，亦即只考虑局部领域内的相似性，如果点 $i$ 和 $j$ 距离太远的话，$S_{ij}$ 应该为零。有两种很直接的办法可以让普通的相似度矩阵具有这种局部性质：

1. 通过设置一个阈值，相似度在阈值以下的都直接置为零，这相当于在一个 $\epsilon$-领域内考虑局部性。
2. 对每个点选取 k 个最接近的点作为邻居，与其他的点的相似性则置为零。这里需要注意的是 LE 要求相似度矩阵具有对称性，因此，我们通常会在 $i$ 属于 $j$ 的 k 个最接近的邻居且/或反之的时候，就保留 $S_{ij}$ 的值，否则置为零。

构造好 $S$ 之后再来考虑降维，从最简单的情况开始，即降到一维 $\mathbf{x}_i \rightarrow y_i$ ，通过最小化如下目标函数来实现：

从直观上来说，这样的目标函数的意义在于：如果原来 $\mathbf{x}_i$ 和 $\mathbf{x}_j$ 比较接近，那么 $W_{ij}$ 会相对比较大，这样如果映射过后 $y_i$ 和 $y_j$ 相差比较大的话，就会被权重 $W_{ij}$ 放大，因此最小化目标函数就保证了原来相近的点在映射过后也不会彼此相差太远。

令 $D$ 为将 $W$ 的每一行加起来所得到的对角阵，而 $L = D-W$ ，被称作是拉普拉斯矩阵，通过求解如下的特征值问题

易知最小的那个特征值肯定是 0 ，除此之外的最小的特征值所对应的特征向量就是映射后的结果。特征向量是一个 N 维列向量，将其旋转一下，正好是 N 个原始数据降到一维之后的结果。

类似地推广到 M 维的情况，只需要取除去 0 之外的最小的 M 个特征值所对应的特征向量，转置之后按行排列起来，就是降维后的结果。用 Matlab 代码写出来如下所示（使用了 knn 来构造相似度矩阵，并且没有用 heat kernel ）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

% Laplacian Eigenmap ALGORITHM (using K nearest neighbors)
%
% [Y] = le(X,K,dmax)
%
% X = data as D x N matrix (D = dimensionality, N = #points)
% K = number of neighbors
% dmax = max embedding dimensionality
% Y = embedding as dmax x N matrix
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
function [Y] = leigs(X,K,d)
 
[D,N] = size(X);
fprintf(1,'LE running on %d points in %d dimensions\n',N,D);
 
 
% STEP1: COMPUTE PAIRWISE DISTANCES & FIND NEIGHBORS 
fprintf(1,'-->Finding %d nearest neighbours.\n',K);
 
X2 = sum(X.^2,1);
distance = repmat(X2,N,1)+repmat(X2',1,N)-2*X'*X;
 
[sorted,index] = sort(distance);
neighborhood = index(2:(1+K),:);
 
 
 
% STEP2: Construct similarity matrix W
fprintf(1,'-->Constructing similarity matrix.\n');
 
W = zeros(N, N);
for ii=1:N
    W(ii, neighborhood(:, ii)) = 1;
    W(neighborhood(:, ii), ii) = 1;
end
 
% STEP 3: COMPUTE EMBEDDING FROM EIGENVECTS OF L
fprintf(1,'-->Computing embedding.\n');
 
D = diag(sum(W));
L = D-W;
 
% CALCULATION OF EMBEDDING
options.disp = 0; options.isreal = 1; options.issym = 1; 
[Y,eigenvals] = eigs(L,d+1,0,options);
Y = Y(:,2:d+1)'*sqrt(N); % bottom evect is [1,1,1,1...] with eval 0
 
 
fprintf(1,'Done.\n');
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

事实上，Laplacian Eigenmap 假设数据分布在一个嵌套在高维空间中的低维流形上， Laplacian Matrix $L$ 则是流形的 Laplace Beltrami operator 的一个离散近似。关于流形以及 Laplacian Eigenmap 这个模型的理论知识就不在这里做更多地展开了，下面看一个比较直观的例子 Swiss Roll 。

Swiss Roll 是一个像面包圈一样的结构，可以看作一个嵌套在三维空间中的二维流形，如下图所示，左边是 Swiss Roll ，右边是从 Swiss Roll 中随机选出来的一些点，为了标明点在流形上的位置，给它们都标上了颜色。

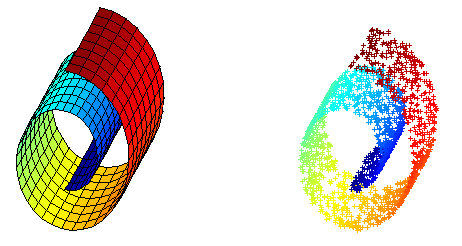
而下图是 Laplacian Eigenmap 和 PCA 分别对 Swiss Roll 降维的结果，可以看到 LE 成功地把这个流形展开把在流形上属于不同位置的点映射到了不同的地方，而 PCA 的结果则很糟糕，几种颜色都混杂在了一起。

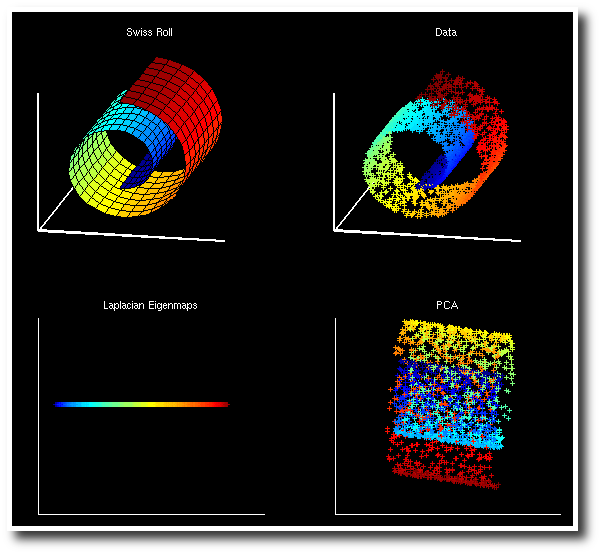
另外，还有一种叫做 Locally Linear Embedding 的降维方法，它同 LE 一样采用了流形假设，并假定平滑流形在局部具有线性性质，一个点可以通过其局部邻域内的点重构出来。首先它会将下式最小化

以求解出最优的局部线性重构矩阵 $W$ ，对于距离较远的点 $i$ 和 $j$ ，$W_{ij}$ 应当等于零。这之后再把 $W$ 当作已知量对下式进行最小化：

这里 $\mathbf{y}$ 成了变量，亦即降维后的向量，对这个式子求最小化的意义很明显了，就是要求如果原来的数据 $\mathbf{x}_i$ 可以以 $W$ 矩阵里对应的系数根据其邻域内的点重构出来的话，那么降维过后的数据也应该保持这个性质。

经过一些变换之后得到的求解方法和 LE 类似，也是要求解一个特征值问题，实际上，从理论上也可以得出二者之间的联系（LE 对应于 $\mathcal{L}$ 而 LLE 对应于 $\mathcal{L}^2$），如果感兴趣的话，可以参考 Laplacian Eigenmaps for Dimensionality Reduction and Data Representation 这篇论文里的对比。下面是两种方法在 Swiss Roll 数据上的结果，也是非常相似的：

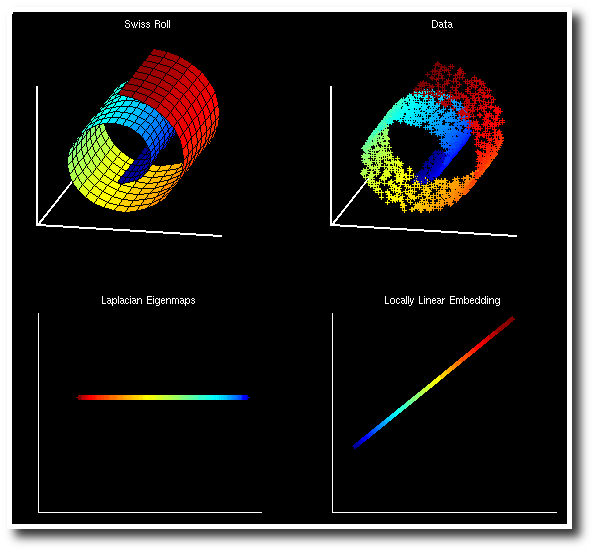
有一点需要注意的是，LE 和 LLE 都是非线性的方法，PCA 得到的结果是一个投影矩阵，这个结果可以保存下来，在之后对任意向量进行投影，而 LE 和 LLE都是直接得出了数据降维之后的结果，但是对于新的数据，却没有得到一个“降维函数”，没有一个合适的方法得到新的数据的降维结果。所以，在人们努力寻求非线性形式扩展 PCA 的时候，另一些人则提出了 LE 和 LLE 的线性形式，分别叫做 Locality Preserving Projection 和 Neighborhood Preserving Embedding 。

在 LPP 中，降维函数跟 PCA 中一样被定为是一个线性变换，用一个降维矩阵 $A$ 来表示，于是 LE 的目标函数变为

经过类似的推导，最终要求解的特征值问题如下：

得到的按照特征值从小到大排序的特征向量就组成映射矩阵 $A$ ，和 LE 不同的是这里不需要去掉第一个特征向量。另一点是在 LE 中的特征值是一个稀疏的特征值问题，在只需要求解最小的几个特征值的时候可以比较高效地求解，而这里的矩阵在乘以 $X$ 之后通常就不再稀疏了，计算量会变得比较大，这个问题可以使用 Spectral Regression 的方法来解决，参见 Spectral Regression: A Unified Approach for Sparse Subspace Learning 这篇 paper 。如果采用 Kernel Trick 再把 LPP 非线性化的话，又会回到 LE 。而 LLE 的线性版本 NPE 也是采用了类似的办法来得到的，就不在这里多讲了。

另外，虽然 LE 是 unsupervised 的，但是如果训练数据确实有标签可用，也是可以加以利用的——在构造相似度矩阵的时候，属于同一类别的相似度要大一些，而不同类别的相似度则会小一些。

当然，除去聚类或分类之外，降维本身也是一种比较通用的数据分析的方法，不过有许多人批评降维，说得到的结果没有意义，不用说非线性，就是最简单的线性降维，除去一些非藏极端的特殊情况的话，通常将原来的分量线性组合一下都不会得到什么有现成的物理意义的量了。然而话也说回来，现在的机器学习几乎都是更 prefer “黑盒子”式的方法吧，比如决策树，各个分支对应与变量的话，它的决策过程其实人是可以“看到”或者说“理解”的，但是 SVM 就不那么“直观“了，如果再加上降维处理，就更加“不透明”了。不过我觉得这没什么不好的，如果只是靠可以清晰描诉出来的 rule 的话，似乎感觉神秘感不够，没法发展出“智能”来啊 ^_^bb 最后，所谓有没有物理意义，其实物理量不过也都是人为了描述问题方便而定义出来的吧。